Површина фигура у равни

Нека је $D$ равна геометријска фигура ограничена затвореном простом кривом $L$. Уписани многоугао у фигуру $D$ је многоугао чије се све тачке налазе у $D$, док је описани многоугао око фигуре $D$ многоугао који садржи све тачке фигуре $D$. Нека је $\{W_u\}$ скуп површина уписаних, а $\{W_o\}$ скуп површина описаних многоуглова фигуре $D$. Скуп $\{W_u\}$ је ограничен одозго, а скуп $\{W_o\}$ ограничен одоздо, па постоје $\sup\{W_u\}=\underline{P}$ и $\inf\{W_o\}=\overline{P}$.

Дефиниција 7. Каже се да је фигура $D$ мерљива ако је $\underline{P}=\overline{P}$. При томе се заједничка вредност $\underline{P}$ и $\overline{P}$ назива површином фигуре $D$ и означава са $P(D)$.

Став 12. Равна фигура $D$ је мерљива ако и само ако за свако $\varepsilon > 0$ постоје описани и уписани многоугао фигуре $D$, тако да је разлика $W_o-W_u$ њихових површина мања од $\varepsilon$.

Нека је у равни задат координатни систем $xOy$. Приликом рачунања површине фигура у равни биће коришћене дефиниција 3, дефиниција 5. и теорема 7, као и дефинисани појам мерљиве фигуре.

1. Нека је на одсечку $[a, b]$ осе $Ox$ дата $f(x)$ која је непрекидна и ненегативна на $[a, b]$. Онда је фигура $F$ у тој равни, ограничена $[a, b]$, $x=a$ и $x=b$ и функције $y=f(x)$ за $x \in [a, b]$. На основу наведених дефиниција и теорема, фигура $F$ ће имати $$P(F)=\int_{a}^{b}{f(x)dx}.$$
   Ovo je Java Applet napravljen u GeoGebri sa www.geogebra.org - izgleda da nemate instaliranu Javu; molim otvorite www.java.com
   
   
2. Нека је функција $g(x)$ на $[a, b]$ непрекидна и непозитивна. Тада ће криволинијски трапез $F$ одређен на као у претходном случају имати $$P(F)=-\int_{a}^{b}{g(x)dx}.$$
   Ovo je Java Applet napravljen u GeoGebri sa www.geogebra.org - izgleda da nemate instaliranu Javu; molim otvorite www.java.com
   
   
3. Ако је функција $f(x)$ на одсечку $[a, b]$ непрекидна и мења знак $c_1, c_2, \ldots, c_k$ онда фигура $F$, ограничена $[a, b]$, $x=a$ и $x=b$ и функције $f(x), x \in [a, b]$, има $P(F)$ која се рачуна као на које је фигуру могуће разложити и који се уклапају у један од прва два случаја.
   
   
   Ovo je Java Applet napravljen u GeoGebri sa www.geogebra.org - izgleda da nemate instaliranu Javu; molim otvorite www.java.com
   
   

   У примеру са аплета било би $$P(F)=P(F_1)+P(F_2)+P(F_3)+P(F_4)=\int_a^{c_1}{f(x)dx}-\int_{c_1}^{c_2}{f(x)dx}+\int_{c_2}^{c_3}{f(x)dx}-\int_{c_3}^{b}{f(x)dx}.$$

4. Нека су на $[a, b]$ осе $Ox$ дате функције $f(x)$ и $g(x)$ које су непрекидне на $[a, b]$ и за свако $x \in [a, b]$ је $g(x) < f(x)$. Нека је $F$ у тој равни дата са $$F=\{(x,y)|a\leq x \leq b, g(x)\leq y \leq f(x)\},$$ као на наредном аплету. На основу претходног, може се закључити да фигура $F$ има $P(F)$ која се рачуна по формули $$P(F)=\int_a^b{(f(x)-g(x))dx}.$$
   
   
   This is a Java Applet created using GeoGebra from www.geogebra.org - it looks like you don't have Java installed, please go to www.java.com
   
   

Пример 1. Израчунати површину дела равни који ограничавају криве $y=\sqrt{x}$, $x+y=2$, $y=0$ и $x=3$.

Решење:

Дата је $y=\sqrt{x}$ и праве , и . Пресечне тачке датих функција су $(1, 1)$ $(3, -1)$ и $(3, \sqrt{3})$. На наредном аплету, између плаве, зелене, црвене и љубичасте линије налази се фигура чију површину треба израчунати.

Међутим, како фигура на аплету не представља криволинијски трапез већ има шпиц у тачки $(2, 0)$ фигура ће бити на два дела- и . Површина целе фигуре биће збир површина две мање фигуре, приказане на претходном аплету. $$P=P_1+P_2=\int_{1}^{2}{(\sqrt{x}-2+x)dx}+\int_{2}^{3}{\sqrt{x}dx}=\frac{2}{3}x^{\frac{3}{2}}|_{1}^{2}-2x|_{1}^{2}+\frac{1}{2}x^2|_{1}^{2}+\frac{2}{3}x^{\frac{3}{2}}|_{2}^{3}=2\sqrt{3}-\frac{7}{6}.$$

Пример 2. Израчунати површину фигуре у равни ограничене елипсом са полуосама $a$ и $b$. Размотрити и специјалан случај када је $a=b=r$.

Решење:

Нека је у равни елипсе дат координатни систем $xOy$ тако да једначина елипсе буде $$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1.$$

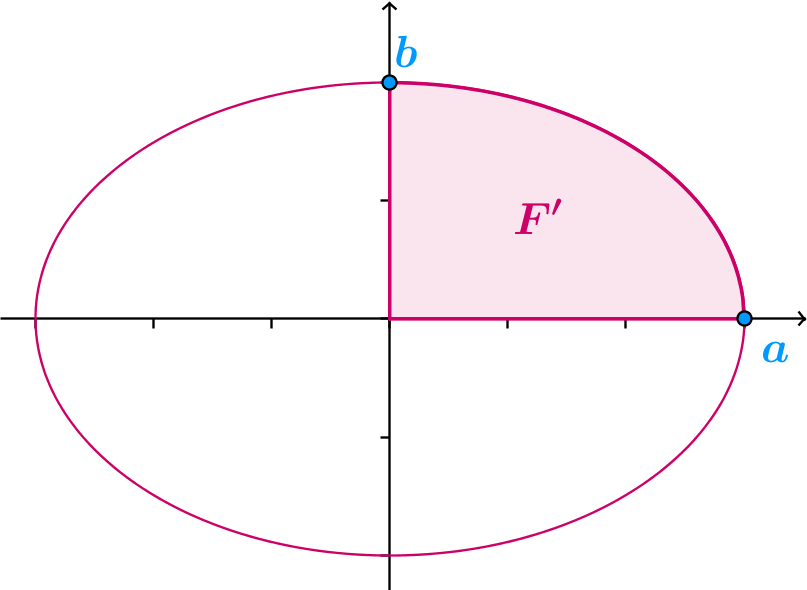
Половина елипсе изнад осе $xOy$ има једначину $$y=\frac{b}{a}\sqrt{a^2-x^2}.$$ Како је наведена функција парна, важиће следеће: $$P(F)=4P(F')=4\int_0^a{\frac{b}{a}\sqrt{a^2-x^2}dx}=4\frac{b}{a}\int_0^a{\sqrt{a^2-x^2}dx}=\left[ \begin{array}{clr} x=a\sin{t} /'\\ dx=a\cos{t}dt\\ x = 0 \longrightarrow t = 0\\ x = a \longrightarrow t = \frac{\pi}{2} \end{array} \right]=$$ $$=4\frac{b}{a}\int_0^{\frac{\pi}{2}}{{\sqrt{a^2-a^2\sin^2{t}}}\cdot a\cos{t}dt} = 4ab\int_0^{\frac{\pi}{2}}{\cos^2{t}dt}=$$ $$=4ab\int_0^{\frac{\pi}{2}}{\frac{1+\cos{2t}}{2}dt}=4ab\left.\left(\frac{t}{2}+\frac{\sin{2t}}{4}\right)\right|_0^{\frac{\pi}{2}}=ab\pi.$$ Ако је специјално, $a=b=r$, одавде се добија позната формула за површину круга $K_r$ полупречника $r$ $$P(K_r)=r^2\pi.$$

Пример 3. Наћи површину равног лика ограниченог графиком функције $f(x)=x^2+x+1$, правом $x=-1$ и тангентом те криве у тачки $A(1, y)$.

Решење:

Прво треба наћи $y$ координату тачке $A$. Она мора да задовољи једначину криве, па ће бити $$y=1^2+1+1=3.$$ Дакле, координате су $A(1, 3)$. Једначина тангенте у тачки на датој криви биће: $$y-y_0=f'(x_0)(x-x_0).$$ Како је $f'(x)=2x+1$, биће $f'(x_0)=3$, па је одатле једначина $y=3x$. Потребно је наћи прво тачке пресека наведених функција. $f$ и $x=-1$ секу се у тачки $(-1, 1)$, а права $x=-1$ и тангента $y=3x$ се секу у тачки $(-1, -3)$. Границе интеграције по $x$ ће бити од -1 до 1.

фигуре ће бити: $$ P=\int_{-1}^{1}{(x^2+x+1)dx}-\int_{-1}^{1}{3xdx}=\left.\frac{x^3}{3}\right|_{-1}^{1}+\left.\frac{x^2}{2}\right|_{-1}^{1}+x|_{-1}^{1}-\left.\frac{3x^2}{2}\right|_{-1}^{1}= $$$$ =\left.\frac{x^3}{3}\right|_{-1}^{1}-x^2|_{-1}^{1}+x_{-1}^{1}=\frac{1}{3}+\frac{1}{3}+1+1=\frac{8}{3}. $$

Пример 4. Наћи површину равног лика ограниченог са $y_1=2-|x-2|$ и $\displaystyle{y_2=\frac{3}{|x|}}$.

Решење:

Потребно је прво разложити апсолутну вредност по дефиницији. $$ |x-2|=\left\{ \begin{array}{rl} x-2, & x \geq 2 \\ 2-x, & x < 2. \end{array} \right. $$ Тада је $$ y_1=\left\{ \begin{array}{rl} 4-x, & x \geq 2 \\ x, & x < 2. \end{array} \right. $$ Пресечне тачке графика $y_1$ и $y_2$ су $(\sqrt{3}, \sqrt{3})$ и $(3, 1)$. Како функција $y_1=2-|x-2|$ има шпиц у тачки $(2, 2)$ површина ће се добити као збир $F_1$ и $F_2$.

Дакле, важи следеће: $$ P=P(F_1)+P(F_2)=\int_{\sqrt{3}}^{2}{\left(x-\frac{3}{x}\right)dx}+\int_{2}^{3}{\left(4-x-\frac{3}{x}\right)dx}= $$$$ =\left.\frac{x^2}{2}\right|_{\sqrt{3}}^{2}-3\ln{x}|_{\sqrt{3}}^{2}+4x|_{2}^{3}-\left.\frac{x^2}{2}\right|_{2}^{3}-3\ln{x}|_{2}^{3}=2-\frac{3}{2}\ln{3}. $$

Пример 5. Израчунати површину фигуре ограничене кривама $\displaystyle{f(x)=\frac{1}{1+x^2}}$ и $\displaystyle{g(x)=\frac{x^2}{2}}$.

Решење:

За почетак ће бити нацртани графици функције и функције . Оне се секу у двема тачкама $\left(-1, \frac{1}{2}\right)$ и $\left(1, \frac{1}{2}\right)$, па ће границе интеграције ићи од -1 до 1.

фигуре ће бити $$P=\int_{-1}^{1}{\left(\frac{1}{1+x^2}-\frac{x^2}{2}\right)dx}.$$ Због парности функције, важи да је $$P=2\int_{0}^{1}{\left(\frac{1}{1+x^2}-\frac{x^2}{2}\right)dx}=\left.2arctg{x}|_{0}^{1}-\frac{x^3}{3}\right|_{0}^{1}=\frac{\pi}{2}-\frac{1}{3}.$$