Прва теорема о средњој вредности

Теорема 11. Нека су $f, g \in \mathcal{R}[a, b]$, $\displaystyle{m = \inf_{x\in[a, b]}{f(x)}}$, $\displaystyle{M = \sup_{x\in[a, b]}{f(x)}}$ и $g(x)\geq0 (g(x)\leq 0)$ за $x\in[a, b]$. Тада постоји $\mu\in[m, M]$, тако да је $$\int_{a}^{b}{f(x)g(x)dx}=\mu\int_{a}^{b}{g(x)dx}.$$ Ако је још и $f\in C[a, b]$, онда постоји $c\in (a, b)$, тако да је $$\int_{a}^{b}{f(x)g(x)dx}=f(c)\int_{a}^{b}{g(x)dx}.$$

Доказ:

Нека је функција $g$ ненегативна. Тада из $m \leq f(x) \leq M$ следи $$\left. mg(x) \leq f(x)g(x) \leq Mg(x), x \in [a, b] \right/\int$$ $$m\int_{a}^{b}{g(x)dx}\leq \int_{a}^{b}{f(x)g(x)dx}\leq M\int_{a}^{b}{g(x)dx}.$$ Ако је $\displaystyle{\int_{a}^{b}{g(x)dx}=0}$, онда је $\displaystyle{\int_{a}^{b}{f(x)g(x)dx}=0}$ и важи $\displaystyle{\int_{a}^{b}{f(x)g(x)dx}=\mu\int_{a}^{b}{g(x)dx}}$. Ако је $\displaystyle{\int_{a}^{b}{g(x)dx}>0}$, онда је $$m\leq\frac{\int_{a}^{b}{f(x)g(x)dx}}{\int_{a}^{b}{g(x)dx}}\leq M,$$ па се за број $\mu$ може узети $\displaystyle{\frac{\int_{a}^{b}{f(x)g(x)dx}}{\int_{a}^{b}{g(x)dx}}}$. У случају непрекидности функције $f$ према Коши-Болцановој теореми о међувредности Нека је $f: [a, b] \longrightarrow \mathbb{R}$ непрекидна функција $f(a)=A$, $f(b) = B$ и $C$ произвољна вредност између $A$ и $B$. Тада постоји тачка $c \in [a, b]$, таква да је $f(c)=C$. постоји тачка $c\in(a, b)$, тако да је $f(c)=\mu$, па једнакост $\displaystyle{\int_{a}^{b}{f(x)g(x)dx}=f(c)\int_{a}^{b}{g(x)dx}}$ важи.

Уколико се у претходној теореми стави да је $g(x)\equiv 1$, добија се последица наведене теореме.

Последица 4. Нека је $f\in \mathcal{R}[a, b]$, $\displaystyle{m = \inf_{x\in [a, b]}{f(x)}}$, $\displaystyle{M = \sup_{x\in [a, b]}{f(x)}}$. Тада постоји $\mu\in[m, M]$ тако да $$\int_{a}^{b}{f(x)dx}=\mu(b-a).$$ Ако је $f\in \mathcal{C}[a, b]$, онда постоји $c\in(a, b)$ тако да важи једнакост $$\int_{a}^{b}{f(x)dx}=f(c)(b-a).$$

Наведена последица се некад назива првом теоремом о средњој вредности и она има своју геометријску интерпретацију. Нек је дат график функције $f(x)$. Постоји $c \in (a, b)$ тако да важи $$\int_{a}^{b}{f(x)dx}=f(c)\cdot (b-a).$$ је вредност функције у тачки $c$. Наведена једнакост казује да је површинa који функција $f(x)$ гради на интервалу $[a, b]$ једнака са површином .

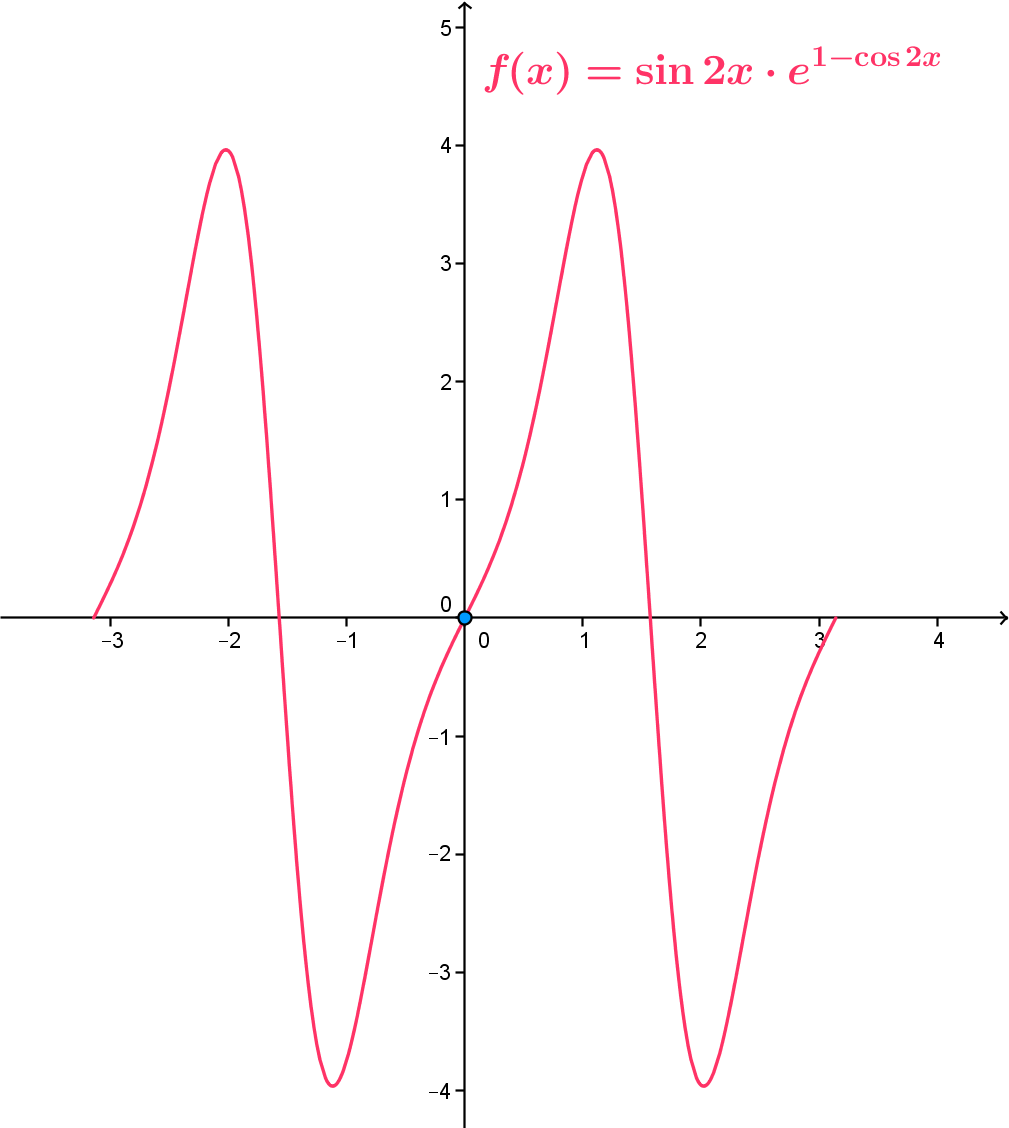
Пример 1. Наћи средњу вредност функције $f(x) = \sin{2x}\cdot e^{1-\cos{2x}}$ на интервалу $[-\pi, \pi]$.

Решење:

Биће примењена теорема о средњој вредности $$f(c)=\frac{1}{b-a}\int_{a}^{b}{f(x)dx}.$$ Види се да је $$f(c)=\frac{1}{2\pi}\int_{-\pi}^{\pi}{\sin{2x}\cdot e^{1-\cos{2x}}dx}.$$ Увођењем смене $t=1-\cos{2x}$, долази се до решења неодређеног интеграла $$\int{\sin{2x}e^{1-\cos{2x}}dx}=\frac{1}{2}\int{e^tdt}=\frac{1}{2}e^t=\frac{1}{2}e^{1-\cos{2x}}.$$ Сада се може наћи средња вредност функције $f$. $$f(c)=\left.\frac{1}{4\pi}e^{1-\cos{2x}}\right|_{-\pi}^{\pi}=0.$$ Добијено је да је средња вредност функције једнака 0, што се може видети и на графику наведене функције.

Пример 2. Наћи број $c$ који задовољава теорему о средњој вредности за функцију $f(x)=x^2+3x+2$, на интервалу $[1, 4]$.

Решење:

Функција $f(x)$ је непрекидна на датом интервалу и могуће је применити теорему о средњој вредности. $$f(c)=\frac{1}{4-1}\int_{1}^{4}{(x^2+3x+2)dx}$$ $$f(c)=\left.\frac{1}{3}(\frac{x^3}{3}+\frac{3}{2}x^2+2x)\right|_{1}^{4}$$ Одавде је $$3(c^2+3c+2)=\frac{99}{2},$$ одакле се добија да је $c_1=2,593$ и $c_2=-5,593$. Број $c_2$ не припада интервалу у коме је тражена средња вредност, па ће решење задатка бити $c_1$.