Površina geometrijskih figura

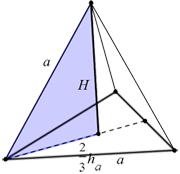Možemo uočiti pravougli trougao i na njega primeniti pitagorinu teoremu:

$H^2 = a^2 - (\frac{2}{3} h_a)^2$
$H^2 = a^2 -(\frac{2}{3} \cdot \frac{a\sqrt{3}}{2})^2$
$H^2 = 9^2 cm^2 - (\frac{9 \sqrt{3}cm}{3})^2$
$H^2 = 81 cm^2 + 27cm^2=108cm^2$
pa je $H=6\sqrt{3}cm .$

Zatvori rešenje.

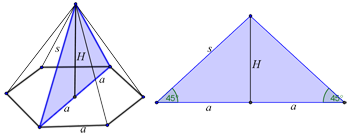Kao i u prethodnom zadatku skicirajmo sliku a onda pogledajmo kako izgleda dijagonalni presek.
Ugao kod vrha piramide je prav, ako spustimo visinu iz vrha piramide ona taj pravougli trougao deli na dva podudarna jednakokraka trougla. Odatle možemo da zaključimo da je visina piramide jednaka osnovnoj ivici $a$, a upotrebom pitagorine teoreme dobijamo:
$s^2=a^2 + H^2$
$6^2 cm^2=2H^2$
$H^2=18cm^2$, odavde sledi da je $H=3\sqrt{2}.$ Zatvori rešenje.

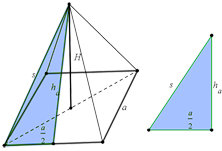Uočimo pravougli trougao i upotrebimo Pitagorinu teoremu da izračunamo $a$:
$(\frac{a}{2})^2 = s^2 -h_a^2$
$(\frac{a}{2})^2 =35^2 cm^2 - 28^2 cm^2$
$(\frac{a}{2})^2 =441cm^2 $
$\frac{a}{2} =21cm,$ odnosno $a=42cm.$
$M=4\cdot\frac{ a\cdot h_a}{2}=2352cm^2$
$B=a^2=1764cm^2$ i površina je:
$P=M+B=2352cm^2 + 1764cm^2=4116cm^2 .$ Zatvori rešenje.

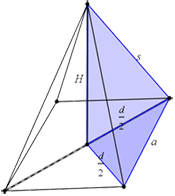Baza nove piramide je jednakokraki pravougli trougao sa katetom $\frac{d}{2} , $ omotač čine dva jednaka pravougla trougla, sa katetama $H$ i $\frac{d}{2}$, i strana stare piramide.
Izračunajmo $d,$
$d^2=2a^2 ,$ $d^2=64cm^2$ pa je $d=8cm.$
Kako bi mogli da izračunamo površinu moramo da odredimo $h_a$
$h_a^2 = (\frac{a}{2})^2 +H^2$
$h_a ^2=8cm^2 + 16cm^2 ,$ $h_a=4\sqrt{6}.$ Pa računamo površinu:
$B=\frac{1}{2}(\frac{d}{2})^2=8cm^2$
$M=2\frac{H\cdot \frac{d}{2}}{2} + \frac{a\cdot h_a}{2}$ Zatvori rešenje.

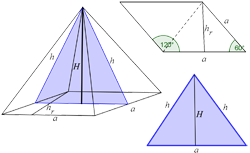Posmatrajmo bazu prizme i primetimo da ako manjom dijagonalom podelimo robm, dobićemo dva jednakostranićna trougla. Visina svakog od trougla biće:
$h_r=\frac{a\sqrt{3}}{2}=3\sqrt{3}cm$, pa je i $H=3\sqrt{3}cm.$
Posmatrajmo presek piramide koroz teme paralelan sa ivicom osnove, izračunajmo visinu stranice piramide
$h^2=H^2 + (\frac{a}{2})^2$
$h^2=27cm^2 + 9cm^2=36cm^2$, pa je $h=6cm.$
$B=a\cdot h_r=6cm \cdot 3\sqrt{3}cm=18\sqrt{3}cm $
$M=4 \cdot \frac{a\cdot h}{2}=72cm^2$
$P=M+B=72cm^2 + 18\sqrt{3}cm^2 .$ Zatvori rešenje.

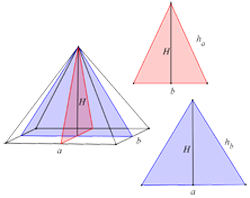Posmatrajmo presek prizme, paralelan ivici $a$. Primenimo Pitagorinu teoremu na pravougli trougao:
$H^2 = h_b^2 - (\frac{a}{2})^2$
$H^2 =26^2 cm^2 - 10^2cm=576cm^2$
$H=24cm.$
Posmatrajmo sada drugi presek, paralelan sa ivicom $b$, izračunajmo visinu stranice $a$
$h_a ^2=H^2 + (\frac{b}{2})^2$
$h_a ^2=576cm^2 + 49cm^2 =625cm^2$
$h_a = 25cm.$
$B=a\cdot b=20cm \cdot 14cm=280cm$
$M=2\cdot (\frac{a\cdot h_a}{2} +\frac{b \cdot h_b}{2})=20cm \cdot 25cm + 14cm \cdot 26cm = 864cm^2 .$
$P=B+M=1144cm^2 .$ Zatvori rešenje.