1. Odredi površinu kocke ako je površina dijagonalnog preseka $16 \sqrt{2}\; cm^2 .$
Dijagonalni presek je pravougaonik sa stranama koje su ivica kocke $a$ i dijagonala strane kocke $d=a \sqrt{2} .$ Pa je $P=a\cdot a\sqrt{2}$
$16\sqrt{2}=a^2 \sqrt{2}$ i odavde sledi da je $a=4.$
Zatvori rešenje.
2. Komad lima je pravougaonog oblika sa dimenzijama $31\; cm$ i $11\; cm.$ Da li se može napraviti kutija oblika kvadra čije su dimenzije $1\; dm,$ $0,6\; dm$ i $11\; dm?$
Izračunajmo površinu lima i površinu kvadra, i uporedimo ih.
$P_{l}=31cm \cdot 11cm=341cm^2 .$
$P_{k}=2(10cm\cdot 6cm + 6cm\cdot 11cm +11cm\cdot 10cm )=2\cdot 236cm^2=472cm^2$
Pošto je površina lima manja od površine kvadra, nije moguće napraviti kvadar.
Zatvori rešenje.
3. Izračunaj $P$ pravilne šestostrane prizme ako je obim većeg dijagonalnog preseka $22\; cm,$ a razlika visine prizme i osnovne ivice $2\; cm.$
Veliki dijagonalni presek je pravougaonik sa stranama $H$ i $2a,$ obim tog pravougaonika je: $O=2(H+2a)$
$22=2(H+2a),$ $11=H+2a.$
A u zadatku je dato i $H-a=2$ odnosno $H=a+2$ ako ovo zamenimo u gornju jednakost dobijamo $11=a+2+2a$, odavde sledi da je $a=3cm$ i $H=5cm.$
$P=2B+M$
$B=6\cdot \frac{a^2 \sqrt{3}}{4}=6\cdot \frac{9 cm^2\sqrt{3}}{4}=13,5 cm^2 \sqrt{3}$
$M=6\cdot a \cdot H=6\cdot 3cm \cdot 5cm=90cm^2$
$P=2B+M=27cm^2\sqrt{3}+90cm^2 .$
Zatvori rešenje.
4. Ako kvadar ivica $18\; cm $, $12\; cm$ i $6\; cm$ izrežemo na kocke ivice $3\; cm,$ koliko se dobija kockica?
Dakle kada svaku stranu kvadra izrežemo na dužinu od $3cm,$ na stranama kvadra dobićemo redom 2, 3, 4 odsečka. A ukupan broj kockica $2\cdot 3\cdot 4=24.$
Zatvori rešenje.
5. Izračunaj površinu prave prizme koja u osnovi ima romb obima $68\; cm$i jedne dijagonale $30\; cm,$ a visina prizme je jednaka drugoj dijagonali osnove.
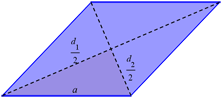Posmatrajmo osnovu prizme, romb, i primenimo pitagorinu teoremu kako bi izračunali drugu dijagonalu . Ako je $O=68cm,$ tada je $a=\frac{O}{4}=17cm .$ $\frac{d_1}{2}=\frac{30cm}{2}=15cm .$Iz pravouglog trougla:
$ (\frac{d_2}{2})^2 =a^2 - (\frac{d_1}{2})^2=17^2 cm^2 -15^2 cm^2=64cm^2, $ pa je
$\frac{d_2}{2}=8cm,$ odnosno $d_2=16cm$ koliko iznosi i $H.$
$P=2B+M,$
$B=\frac{d_1 \cdot d_2}{2}=\frac{30cm \cdot 16cm}{2}=240cm^2,$
$M=4\cdot a\cdot H=4\cdot 17cm \cdot 16cm=1088cm^2$
$P=2B+M=480cm^2 + 1088cm^2 =1568cm^2 .$ Zatvori rešenje.
6. Izračunaj $P$ pravilne šestostrane jednakoivične prizme ako je površina omotača $96\; cm^2 .$
To što je piramida pravilna jednakoivična znači da su ivice i visina jednake. Pa:
$P_{omotaca}=6\cdot a \cdot H$
$96cm^2=6\cdot a^2$
$a^2=36cm^2,$ pa odavde sledi da je $a=6cm.$
Računamo površinu omotača:
$M=6\cdot \frac{a^2\sqrt{3}}{4}=54\sqrt{3} cm^2 .$ A površina je:
$P=2B+M=192cm^2 + 54\sqrt{3}cm^2 .$
Zatvori rešenje.
7. Izračunaj $P$ prizme koja u osnovi ima pravougli trougao kateta $12\; cm$ i $9\; cm,$ a najveća bočna strana je kvadrat najveće moguće veličine.
Pre svega odredimo hipotenuzu pravouglog trougla u osnovi prizme.
$c^2 = 12^2 cm^2 + 9^2 cm^2= 225cm^2 ,$ $c=15cm.$ Zaključujemo da je visina prizme $H=15cm.$
$P=2B+M$
$B=\frac{12cm\cdot 9cm}{2}=54cm^2 ,$
$M=15cm \cdot (15cm+ 9cm +12cm)=540cm^.$
$P=108cm^2 + 540cm^2=648cm^2 .$
Zatvori rešenje.
8. Izračunaj $P$ pravilne trostrane prizme ako je površina jedne bočne strane $54\; cm^2 ,$ a visina prizme je $9\; cm .$
Ako je površina bočne strane $54cm^2$ a visina prizme $9cm,$ tada je ivica osnove piramide $a=\frac{P_{bocne strane}}{H}=\frac{54cm^2}{9cm}=6cm.$
$B=\frac{a^2 \sqrt{3}}{4}=9cm^2 \sqrt{3},$
$M=3\cdot P_{bocne strane}=3\cdot 54cm^2=162cm^2 ,$
$P=2B+M=18cm^2 \sqrt{3} + 162cm^2 .$
Zatvori rešenje.
Posmatrajmo osnovu prizme, romb, i primenimo pitagorinu teoremu kako bi izračunali drugu dijagonalu . Ako je $O=68cm,$ tada je $a=\frac{O}{4}=17cm .$ $\frac{d_1}{2}=\frac{30cm}{2}=15cm .$Iz pravouglog trougla: