Površina proizvoljne figure $F$
Neka je $F$ jedna figura. Za svaki poligon $U$ sadržan u toj figuri rećićemo da je u nju upisan z a za svaki poligon $V$ koji sadrži, obuhvata figuru $F$ rećićemo da je oko nje opisan .
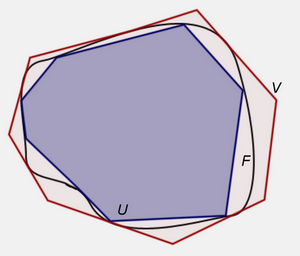
Ako za neku figuru $F$ postoji jedan niz upisanih poligona $U_m$ i niz opisanih poligona $V_m, \; m\in N,$ tako da razlika površine $m-$tog opisanog i $m-$tog upisanog poligona teži $0$ kada $m \rightarrow \infty$. $$\lim_{m \rightarrow \infty} [P(V_m) - P(U_m)]=0,$$ $$P(F)=P(V_m)=P(U_m), m \rightarrow \inf ,$$ tada kažemo da postoji površina figure $F$.
To znači da ako su $M_n, \; n\in N$ i $S_n,\; n\in N, $ Neki drugi niz upisanih i opisanih poligona za figuru F i ako važi: $$\lim_{n\rightarrow \infty} [P(M_n) -P(S_n)]=0,$$ nizovi $P(S_n)$ i $P(M_n), \; n\rightarrow \infty ,$ teže broju $P(F).$ Tada broj $P(F)$ nazivamo površina figure $F .$