Površina ravnog lika
Koristeći se osobinama određenog integrala i zaključaka do kojih smo doši na prethodnoj strani, dobijamo sledeće korisne formule:
Površina ravne površi ograničene osom $Ox,$ krivom $y=f(x)$ i pravim $x=a$ i $x=b,$ definiše se formulom: $$P=\int_{a}^{b} |f(x)| dx.$$ 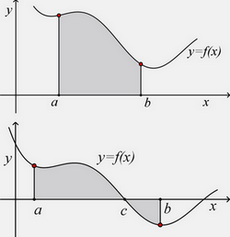
Primetimo da ako je funkcija $f(x) \leq 0$ tada je gornja formula $$P=\int_{a}^{b} f(x) dx.$$ A ako u okviru intervala $[a,b]$ funkcija $f(x)$ menja znak u tački $c$, tada formula postaje $$P=\int_{a}^{c} f(x) dx - \int_{c}^{b} f(x) dx.$$
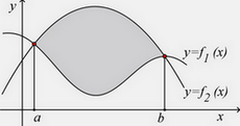
Ako je površ ograničena sa dve krive i neka su tačke $x_1$ i $x_2$ rešenja jednačine $f_1 (x)=f_2 (x),$ tada je površina te površi: $$P=\int_{x_1}^{x_2}f_2 (x)dx - \int_{x_1}^{x_2}f_1 (x)dx=$$ $$\int_{x_1}^{x_2} |f_2 (x) - f_1(x)|dx$$