Površina proizvoljne figure $F$
U četvrtom razredu učenici se susreću sa velikim nastavnim temama izvod i integral, u okviru njih je i nastavna jedinica određen integral. Ovog trenutka i na ovom mestu nećemo se baviti problemima uvođenja ovih pojmova i svim njegovim osobinama, već samo primenom određenog integrala na izračunavanje površine ravnih i krivih likova.
Inače, prvi problem za čije reševanje je upotrebljen određen integral jeste problem izučavanja površi ravnih figura.
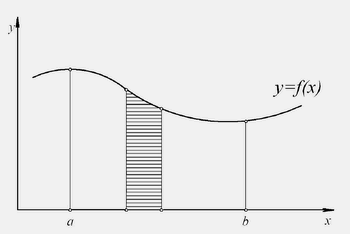
Podsećamo učenike na termin krivolinijski trapez. To je svaka figura u ravni $Oxy$ koja je ograničena krivom $y=f(x),$ $x\in [a,b],$ pravim linijama $x=a,$ $x=b$ i $x$ osom. Površinu takve figure računamo kao:
Definicija Neka je funkcija definisana i neprekidna na odsečku $[a,b]$ i neka je $f(x) \geq 0, $ $x\in [a,b].$ Tada je površina $P$ krivolinijskog trapeza ispod krive $y=f(x),$ nad odsečkom $[a,b]$ jednaka određenom integralu nad odsečkom $[a,b],$ tj: $$P= \int_{a}^{b} f(x)dx.$$
Prirodno je zahtevati da je površina dve figure jednaka zbiru njihovih površina. S obzirom da se većina figura koje srećemo u svakodnevnom radu može predstaviti kao konačna unija krivolinijskih trapeza $$F=F_1 \cup F_2 \cup ... \cup F_k , k\in N ,\quad F_i \cap F_j=0, \quad i,j\leq k.$$ definišemo površinu figure $F$ kao $$P(F)=P(F_1)+P(F_2)+ ... +P(F_k).$$
Prisetimo se definicije površine sa početka ovih stranica
Definicija. Neka je $P$ skup svih poligona u ravni, uključujući
i prazan skup. Površina na skupu $P$ je preslikavanje $p : P \rightarrow R,$ koje ima sledeća svojstva
1. $p(P)\geq 0,$ za svaki poligon $P$.
2. Ako je poligon $P$ unija disjunktnih poligona $P_1$ i $P_2,$ tada je $p(P_1 + P_2)=p(P_1)+p(P_2).$
3. Ako su poligoni $P_1$ i $P_2$ podudarni likovi, tada je $p(P_1)=p(P_2).$
4. Ako je $K$ kvadrat čija je stranica dužine 1, tada je $p(K)=1.$
Broj $p(P)$ se naziva površina poligona $P$.