Zanimljivi zadaci
Grupni rad
Zadaci za naprednije
Osnovni zadaci
1. Krov kuće se sastoji od četiri jednakokraka trougla osnovice $4 m$ i visine $3,2 m.$ Koliko je kvadratnih metara lima potrebno zanjegovo prekrivanje? (Računaj da $10 \%$ materijala otpada.)
Odredimo površinu jednog trougla:
$P=\frac{4m \cdot 3,2m}{2}=6,4m^2 .$
Površina celog krova je $4 \cdot 6,4m^2=25,6m^2 .$
Izračunajmo koliko je $10 \%$ od površine celog krova: $\frac{25,6m^2}{10}=2,56m^2 .$ I konačno da bi prekrili krov, potrebno nam je $25,6 m^2 + 2,56m^2 = 28,16m^2 $ lima.
Zatvori rešenje.
2. Uporedi površine dva trapeza na koje je srednja linija trapeza podelila trapez čije su osnovice $a=12 cm$ i $b=6cm.$ ?
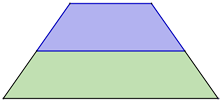 Odredimo srednju liniju $m=\frac{a+b}{2}=9cm .$ Osnovice gornjeg trapeza biće $a=9cm, b=6cm ,$ a osnovice donjeg $a=12cm, b=9cm ,$ visina je kod oba trapeza jednaka i smatraćemo da je $h$.
Odredimo srednju liniju $m=\frac{a+b}{2}=9cm .$ Osnovice gornjeg trapeza biće $a=9cm, b=6cm ,$ a osnovice donjeg $a=12cm, b=9cm ,$ visina je kod oba trapeza jednaka i smatraćemo da je $h$.
$P_{donjeg}=\frac{12cm+9cm}{2}\cdot h=10,5 cm \cdot h $
$P_{gornjeg}=\frac{9cm+6cm}{2}\cdot h=7,5 cm \cdot h $
Veći je gornji trapez, $P_{gornjeg} > P_{donjeg} .$
Zatvori rešenje.
3. Površina trapeza $ABCD$ $(AB || DC)$ je $49 cm^2 .$ Ako je $AB=8 cm$ i $AB : DC=4 : 3,$ kolika je visina tog trapeza?
Izračunajmo prvo dužinu stranice $DC:$
$AB : DC=4 : 3,$
$8cm : DC=4 : 3,$
$DC=\frac{8cm \cdot 3}{4}=6cm.$ A sad visinu:
$49cm^2=\frac{8cm + 6cm}{2}\cdot h$
$h=\frac{49cm^2}{7cm}=7cm.$ Visina je $7cm.$
Zatvori rešenje.
4. Dužina jedne dijagonale romba je tri puta manja od dužine druge dijagonale. Ako je zbir dužina dijagonala $20 cm,$ izračunaj površinu romba.
Odredimo prvo dužine dijagonala
$d_1 + d_2=20cm$
$d_1=3 d_2$, zamenimo ovo u gornju jednačinu
$3d_2 + d_2=20cm$, odavde sledi da je
$d_2=5cm,$ a $d_1=15cm.$ A sad izračunajmo površinu romba
$P=\frac{d_1 \cdot d_2}{2}=\frac{5cm \cdot 15cm}{2}=37,5 cm^2 .$
Zatvori rešenje.
5. Stranice pravougaonika imaju dužinu $12 cm$ i $6 cm.$ Za koliko treba manju stranicu povećati, a veću za isto toliko skratiti da se dobije kvadrat? Za koliko je površina pravougaonika manja od tog kvadrata?
Primetimo da ako i dužu stranicu smanjimo za 3 a manju povećamo za 3 biće jednake i njihove dužine iznose $9cm$.
$P_{p}= 12cm \cdot 6cm=72cm ,$
$P_{k}=9cm \cdot 9cm =81cm^2 .$
Odredimo razliku površina:
$P_{k}-P_{p}=81cm^2 - 72cm^2 =9cm^2 .$
Zatvori rešenje.
6. Postoji samo jedan kvadrat kod koga je merni broj površine jednak mernom broju obima. Odredi dužinu stranica tog kvadrata.$
Dakle $P_{k}=O_{k}$
$a \cdot a=4 \cdot a$, odavde zaključujemo da je
$a=4.$
Zatvori rešenje.
7. Oko travnjaka oblika kvadrata obima $40 m$ napravljena je staza širine $2 m.$ Kolika je površina staze?
 Da bi izračunali površinu staze, računaćemo prvo površinu kvadrata koga čine staza i travnjak i od njega oduzeti površinu kvadrata travnjaka.
Da bi izračunali površinu staze, računaćemo prvo površinu kvadrata koga čine staza i travnjak i od njega oduzeti površinu kvadrata travnjaka.
$P_{s+t}=44m \cdot 44m=1936m^2 ,$
$P_{t}=40m \cdot 40m = 1600m^2 . $
$P_{s}= P_{s+t}-P_{t}=1936m^2 - 1600m^2=336m^2 .$
Zatvori rešenje.
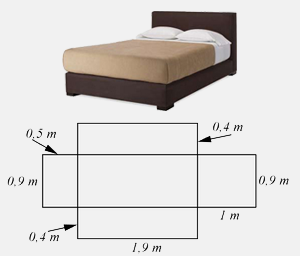 8. Stolar Marko je dobio naruđbinu da napravi krevet prikazan na crtežu.
8. Stolar Marko je dobio naruđbinu da napravi krevet prikazan na crtežu.
a) Kolika je ukupna površina drvenih delova od kojih se sastavlja krevet?
b) Da li je za izradu ovog kreveta dovoljno kupiti jednu drvenu ploču oblika pravougaonika dimenzija $280 cm$ i $210 cm.$
v) Cena $1m^2$ materijala potrebnog za izradu kreveta je 900 din. Koliko košta izrada kreveta, ako zanamo da majstoru Marku treba platiti $50 \%$ cene materijala?