1. Kolika je jedna stranica pravougaonika, ako je njegova površina $340 dm^2$ a dužina druge stranice iznosi $17 dm$?
Površinu pravougaounika računamo kao $P=a\cdot b $
$$340dm^2=a\cdot 17dm$$
$$a=\frac{340dm^2}{17dm}=20dm.$$
Zatvori rešenje.
2. Koliko je potrebno stakla za novu zgradu koja ima $24$ stana a u svakom stanu po $10$ prozora veličine $1.5 m$ i $80 cm$ ?
Izračunajmo površinu jednog prozora $P=1,5m \cdot 0,8m=1,2m^2 .$ U svakom stanu ima po 10 prozora, tako da je ukupno stakla potrebno za svaki stan $1,2m^2 \cdot 10=12m^2 .$ A pošto cela zgrada ima $24$ stana, ukupna površina stakla potrebna za celu zgradu iznosi $12m^2 \cdot 24=288m^2 .$
Zatvori rešenje.
3. Traka dužine $5dm$ ima površinu $1050cm^2 .$ Kolika je širina te trake?
Traka je oblika pravougaonika.
$$P=a\cdot b ,$$
$$1050cm^2=50cm \cdot b,$$
$$b=\frac{1050cm^2}{50cm}=20cm.$$ Širina trake je $20$ centimetara.
Zatvori rešenje.
4. Kolika je površina jednakokrakog trougla čiji je krak $6,5 cm$ a visina koja odgovara kraku $4 cm$?
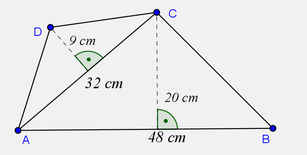
Površinu četvorougla $ABCD$ računamo kao zbir površina dva trougla $ABC$ i $ACD.$ $P_{ABC}=\frac{20cm \cdot 48cm}{2}=480cm^2 ,$
$P_{ACD}=\frac{32cm \cdot 9cm}{2}=144cm^2 ,$
pa je $P_{ABCD}=480cm^2 + 144cm^2= 624cm^2 .$
Zatvori rešenje.
6. Osnovica jednakokrakog trougla je $2,4 m$ a visina koja joj odgovara $3 m.$ Kolika je dužina kraka ako je visina koja mu odgovara $1,8 m?$
Pošto nam je u zadatku data osnovica i visina koja joj odgovara možemo izračunati površinu trougla $P=\frac{a\cdot h_a }{2}=\frac{2,4m \cdot 3m}{2} =3,6m^2 .$ Sada možemo odrediti dužinu kraka: $P=\frac{b \cdot h_b }{2}$
$3,6m^2=\frac{b \cdot 1,8m }{2}$
$b=\frac{3,6 m^2 \cdot 2}{1,8m}=4m$
Zatvori rešenje.
7. Kolika je dužina srednje linije, a kolika površina trapeza, čije su osnovice $24 cm$ i $20 cm$ a visina $9cm?$
9. Ako je u trouglu visina za $2 dm$ veća od stranice kojoj odgovara, a ukupna dužina im je $12dm$, odredi površinu tog trougla.
Prvo moramo da oktrijemo dužine visine i stranice
$a + h_a =12dm$
$h_a=a +2dm$ sada $h_a$ zamenimo u gornju jednačinu,
$a+a+2dm=12dm $ odavde sledi da je
$a=5dm , h_a=7dm$ a površina je
$P=\frac{a \cdot h_a}{2}=\frac{5dm \cdot 7dm}{2}=17,5dm^2 .$
Zatvori rešenje.
10. Od dve daščice dužine $45 cm$ i $22 cm$ dečak je napravio zmaja u obliku deltoida. Koliko je utrošeno $cm^2$ hartije za prekrivanje zmaja?
Ove daščice predstavljaju dijagonale deltoida: $P=\frac{d_1 \cdot d_2}{2}=\frac{45cm\cdot 22cm}{2}=495cm^2 .$
Zatvori rešenje.
11. Dijagonale romba su $5 cm$ i $ 10 cm.$ Izračunaj površinu tog romba, i dužinu stranice kvadrata čija je površina jednaka površini datog romba.
Računamo površinu romba: $P_{romba}=\frac{d_1 \cdot d_2}{2}=\frac{5cm\cdot 10cm}{2}=25cm^2 .$
Kako je $P_{kvadrata}=P_{romba}=25cm^2$ tada je
$a\cdot a=25cm^2$ pa je stranica kvadrata $a=5cm.$
Zatvori rešenje.
12. Ako je u jednom trapezu gornja osnovica $82 mm,$ srednja linija $96 mm$ i visina $5 cm.$ Kolika je površina, kolika je donja osnovica?
Odredimo donju osnovicu: $m=\frac{a+b}{2}$ $96mm=\frac{a+ 82mm}{2}$ $a=2\cdot 96mm - 82mm=100mm$ donja osnovica je $100mm .$
Izračunajmo površinu $P=m\cdot h=96mm \cdot 50mm=4800mm^2 .$
Zatvori rešenje.
13. Od metalne ploče pravougaonog oblika, stranica $2,5 m$ i $3 m,$ treba izrezati postolje u obliku deltoida, ali tako da rastojanje suprotnih temena bude $3 m$ i $2,4 m.$ Koji će procnat ploče biti iskorišćen?
Izračunajmo prvo površinu ploče a zatim i postolja,
$P_{ploce}=2,5m \cdot 3m =7,5 m^2 .$
$P_{postolja}= \frac{3m \cdot 2,4m}{2}=3,6 m^2 .$
A sada proporcijom odredimo koliko smo materijala iskoristili
$P_{ploce} : 100 \% = P_{postolja} : X$
$X=\frac{P_{postolja}}{P_{ploce}} \cdot 100 \%= 48 \%$
Zatvori rešenje.
