Elementarne funkcije
Elementarne funkcije su funkcije koje se mogu dobiti iz osnovnih elementarnih funkcija pomoću konačnog broja aritmetičkih operacija (+, -, ⋅, :) i konačnog broja kompozicija elementarnih funkcija.
Osnovne elementarne funkcije su:
Inverzne trigonometrijske funkcije
Pojam inverznih trigonometrijskih funkcija
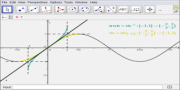
Arkus-funkcijama od $x$(inverznim trigonometrijskim) nazivamo veličine
$y$ merene u radijanima, određene jednačinama:
$$x = \sin f(x) \Rightarrow f(x)=\arcsin x (arkus-sinus)$$
$$x = \cos f(x) \Rightarrow f(x)=\arccos x (arkus-kosinus)$$
$$x = \tan f(x) \Rightarrow f(x)=\arctan x (arkus-tangens)$$
$$x = \cot f(x) \Rightarrow f(x)=arccot x (arkus-kotangens)$$
Glavne vrednosti arkus funkcije su višeznačne. Njihove glavne vrednosti
su ograđene. Označavamo ih sa $\arcsin x, \arccos x, \arctan x$, arccot x, (posled-
nje dve, mi često označavamo $arctg x$, $arcctg x$).
$$-\frac{\pi}{2} \leq \arcsin x \leq \frac{\pi}{2}, 0 \leq \arccos x \leq \pi$$
$$-\frac{\pi}{2} \leq \arctan x \leq \frac{\pi}{2}, 0 \leq arccot x \leq \pi$$






