Помоћни резултати из еуклидске геометрије »
|
| Потенција тачке у односу на круг » |
|
| Инверзија у односу на круг » |
Помоћни резултати из комплексне анализе »
Аксиоме хиперболичке геометрије равни »
Конструкција Поенкареовог диск модела »
Провера аксиома у Поенкареовом диск моделу »
Карактеристике хиперболичке равни у Поенкареовом диск моделу »
Примери »
„Визуелизација Поенкареовог диск модела коришћењем програмског пакета GeoGebra“
Марина Јовановић,
Универзитет у Београду, Математички факултет
Инверзија у односу на круг
Дефиниција: Нека је $k(O,r)$ круг еуклидске равни $\mathbb{E}^2$. Пресликавање $\psi_k:\mathbb{E}^2\setminus\{O\}\rightarrow \mathbb{E}^2\setminus\{O\}$ дефинисано са:
$\psi_k(X)=X'\Leftrightarrow X'$ припада полуправој $OX$ и $OX\cdot OX'=r^2$,
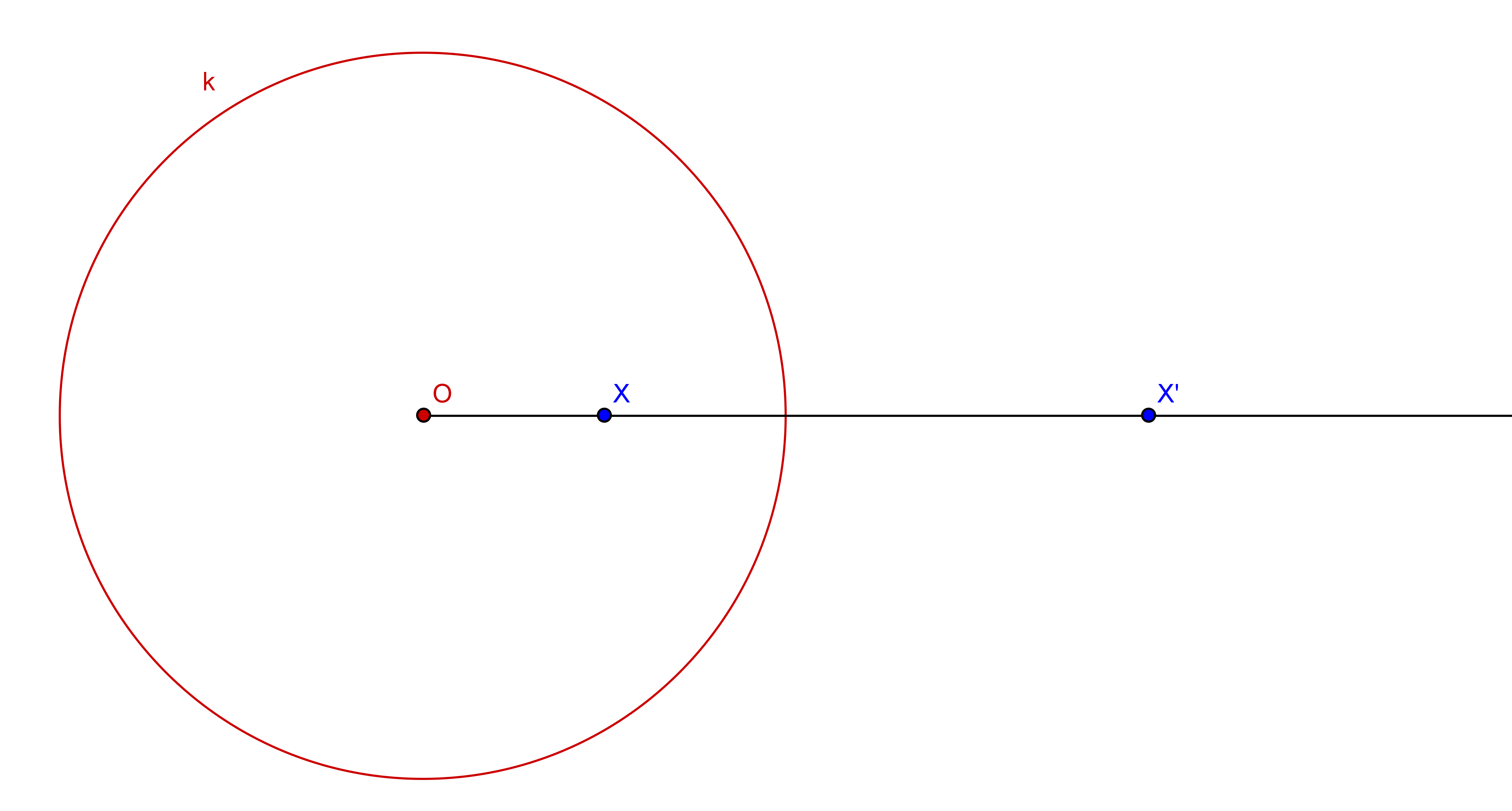
називамо инверзија у односу на круг $k$. Круг $k$ називамо круг, тачку $O$ и полупречник $r$ полупречник инверзије $\psi_k$ (Слика 1).
 |
||
| Слика 1. Инверзија о односу на круг $k$, при чему важи $\psi_k(X)=X'$ |
Напомена:
Зашто је и домен и кодомен овог пресликавања скуп $\mathbb{E}^2\setminus\{O\}$?
Ако би центар $O$ имао своју слику $O'$, тада би на основу дефиницеије инверзије важило:
$\psi_k(O)=O '\Leftrightarrow O '$ припада полуправој $OO$ и $OO\cdot OO '=r^2$.
Међутим, како је дужина дужи $OO '$ једнака $0$, немогуће је да тачка $O$ има слику у инверзији $\psi_k$. Са дрзге стране, тачка $O$ није слика ниједне тачке.
Сада ћемо видети како можемо конструисати слику произвољне тачке $P$ у инверзији $\psi_k$ у односу на круг $k(O,r)$.
Напомена:
Уносом координата тачке $P$ на аплету вам се приказује слика тачке $P$ у инверзији $\psi_k$ у односу на круг $k(O,r)$. Даље, померањем клизача $r$, који представља дужину полупречника круга $k$, можете видети да слика тачке $P$ у инверзији $\psi_k$ директно зависи од полупречника круга $k$ (што и следи из дефиниције инверзије).
Осим уносом нових координата, тачку $P$ је могуће померати и помоћу миша.
Теорема: Инверзија је бијективно пресликавање.
Теорема: Инверзија је инволуција.
Теорема: Инверзија у односу на круг $k(O,r)$ пресликава унутрашњу област тог круга без центра $O$ у његову спољашњост, и обратно (спољашња област круга се инверзијом у односу на тај круг пресликава у унутрашњу област круга без центра $O$).
Следећи аплет нам описује претходне три теореме.
Напомена:
На аплету су дате оригиналне тачке (плаве тачке) и њихове слике (црвене тачке). Померањем плавих тачака можете приметити следеће:
- уколико се дата тачка налази у унутрашњости круга $k$, њена слика се налази у спољашњости круга $k$,
- уколико се дата тачка налази у спољашњости круга $k$, њена слика се налази у унутрашњости круга $k$ и
- уколико се дата тачка налази на граници круга $k$, тада је она поклапа са својом сликом.
На основу претходног аплета можемо закључити да важи следећа теорема:
Теорема: Све инваријантне тачке инверзије су на кругу те инверзије.
Сада ћемо видети како можемо конструисати слику дате тачке у инверзији у односу на дати круг $k(O,r)$.
Следеће теореме ћемо доказати визуелно, тј. помоћу одговарајућих аплета.
Теорема: Нека је дата инверзија ${\psi}_{k}$ у односу на круг $k(O,r)$ и нека је $p$ дата права. Тада важи:
- Ако права $p$ садржи центар инверзије $O$, онда је слика праве $p$ без тачке $O$ у инверзији ${\psi}_{k}$ права $p$ без тачке $O$.
- Ако права $p$ не садржи центар инверзије $O$, онда је слика праве $p$ у инверзији ${\psi}_{k}$ круг $p'$ који садржи тачку $O$, али без тачке $O$.
Напомена:
Осим директним уносом једначине праве $p$, праву $p$ је могуће померати и помоћу миша.
Теорема: Нека је дата инверзија ${\psi}_{k}$ у односу на круг $k(O,r)$ и нека је дат произвољан круг $l$. Тада важи:
- Ако круг $l$ садржи центар инверзије $O$, онда је слика круга $l$ без тачке $O$ у инверзији ${\psi}_{k}$ права $l' $ која не садржи тачку $O$.
- Ако круг $l$ не садржи центар инверзије $O$, онда је слика круга $l$ без тачке $O$ у инверзији ${\psi}_{k}$ круг $l' $ који не садржи тачку $O$.
Напомена:
Осим директним уносом једначине круга $l$, круг $l$ је могуће померати и помоћу миша.


