„Визуелизација Поенкареовог диск модела коришћењем програмског пакета GeoGebra“
Марина Јовановић,
Универзитет у Београду, Математички факултет

Помоћни резултати

из комплексне анализе

      Познато је да еуклидску раван ${\mathbb{E}}^{2}$ можемо идентификовати са скупом комплексних бројева $\mathbb{C}$. Скуп комплексних бројева $\mathbb{C}$ називамо још и комплексна раван. При томе, свакој тачки еуклидске равни одговара тачно један комплексан број, односно једна тачка у комплексној равни. Сваку геометријску фигуру еуклидске равни, тада, видимо као скуп комплексних бројева са неким својством.

      Ради конструкције Поенкареовог диск модела потребни су нам, пре свега, праве и кругови. Стога ћемо видети како изгледају једначине праве и круга у скупу комплексних бројева.

      Праву и круг у скупу комплексних бројева задајемо истом једначином. Односно једначином облика $$Ez\overline{z}+F\overline{z}+\overline{F}z+G=0,$$ при чему су $E,G\in \mathbb{R}$, $F\in \mathbb{C}$ и важи ${|F|}^{2}-EG>0$.

      Фигура задата оваквом једначином назива се уопштени круг.

      Како бисмо показали да је Поенкареов диск модел заиста модел хиперболичке равни потребно је проверити да су на тако дефинисаном моделу задовољене све аксиоме хиперболичке геометрије равни. Из тог разлога потребно је нагласити да смо апсолуту дефинисали као круг комплексне равни,тј као скуп $\{z\in \mathbb{C}: |z| < 1 \}$. Разлог за то је, између осталог, због лакшег проверавања аксиома хиперболичке геометрије. Поћи ћемо од једначине уопштеног круга:
$$Ez\overline{z}+F\overline{z}+\overline{F}z+G=0,E,G\in \mathbb{R},F\in \mathbb{C},{|F|}^{2}-EG>0.$$ Како је $F$ комплексан број, то можемо број $F$ написати на следећи начин: $$F=a+b\cdot i ,a,b\in \mathbb{R}.$$ Пошто је наш модел круг полупречника $1$, извешћемо једначину круга написаног помоћу $x$ и $y$ координата неке тачке.
      Нека је $z=x+y\cdot i$ , $E$ реалан број и $F$ комплексан број облика $F=a+b\cdot i$, где су $a$ и $b$ реални бројеви.
Тада важи:
$$E\cdot z\cdot \overline{z}+\overline{F}\cdot z+F\cdot \overline{z}+G=0$$ $$\Leftrightarrow E\left(x^2+y^2\right)+\left(a-bi\right)(x+yi)+(a+bi)(x-yi)+G=0$$ $$\Leftrightarrow Ex^2+Ey^2+ax+ayi-bxi+by+ax-ayi+bxi+by+G=0$$ $$\Leftrightarrow Ex^2+Ey^2+2ax+2by+G=0$$ На следећем аплету можете доделити вредности параметрима $E$, $a$, $b$ и $G$ видети како изгледа уопштени круг који одговара тако датим параметрима.
Ovo je Java Applet napravljen u GeoGebri sa www.geogebra.org - izgleda da nemate instaliranu Javu; molim otvorite www.java.com

      Лема: Круг са центром $\rho {e}^{i\theta}$ $(\rho >1)$ и полупречником $r$ нормалан је на круг $|z|=1$ ако и само ако је
$$\displaystyle r=\sqrt{{\rho}^{2}-1}.$$

      Доказ: Означимо са ${k}_{1}$ круг $|z|=1$, а са ${k}_{2}$ круг $|z-\rho {e}^{i\theta}|=r$. Даље, означимо са $O$ центар круга ${k}_{1}$, са $C$ центар круга ${k}_{2}$ и са $A$ и $B$ пресечне тачке кругова ${k}_{1}$ и ${k}_{2}$ (Слика 1).

Слика 1. Међусобно нормални кругови $|z|=1$ и $|z-\rho {e}^{i\theta}|=r$

Како су кругови ${k}_{1}$ и ${k}_{2}$ међусобно нормални, то је угао $\angle CAO$ прав, па на основу Питагорине теореме можемо закључити да је ${\rho}^{2}={r}^{2}+{1}^{2}$. Односно, следи да је $\displaystyle r=\sqrt{{\rho}^{2}-1}$.
      Нека су дати кругови ${k}_{1}=\{z\in \mathbb{C}:|z|=1\}$ и ${k}_{2}=\{z\in \mathbb{C}:|z-\rho {e}^{i\theta}|=r,\rho >1\}$, при чему је $\displaystyle r=\sqrt{{\rho}^{2}-1}$. Докажимо прво да се кругови ${k}_{1}$ и ${k}_{2}$ секу (Слика 2).

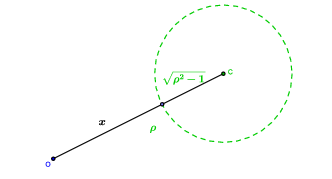Слика 2. Испитивање да ли се кругови $|z|=1$ и $|z-\rho {e}^{i\theta}|=r$ секу

Нека је $x$ растојање центра круга ${k}_{1}$ од круга ${k}_{2}$. Како је $r=\sqrt{{\rho}^{2}-1}$ и $x+r=\rho$, следи да је $x+\sqrt{{\rho}^{2}-1}=\rho$. Сређивањем датог израза добијамо: $$\sqrt{{\rho}^{2}-1}=\rho-x\quad {/}^{2}$$ $${\rho}^{2}-1={\rho}^{2}-2x\rho+{x}^{2}$$ $${x}^{2}-2x\rho+1=0.$$ Даље, решавањем квадратне једначине до које смо дошли (${x}^{2}-2x\rho+1=0$) добијамо $${x}_{1,2}=\frac{2\rho\pm \sqrt{4{\rho}^{2}-4}}{2}=\frac{2\rho\pm 2\sqrt{{\rho}^{2}-1}}{2}=\rho\pm\sqrt{{\rho}^{2}-1}.$$
Како је $\rho>1$, следи да је $\rho+\sqrt{{\rho}^{2}-1}>1$, па нам остаје да испитамо да ли је $\rho-\sqrt{{\rho}^{2}-1}<1$. Решимо неједначину $\rho-\sqrt{{\rho}^{2}-1}<1$. $$\sqrt{{\rho}^{2}-1}>\rho-1 \quad {/}^{2}$$ $${\rho}^{2}-1>{\rho}^{2}-2\rho +1$$ $$-2>-2\rho$$ односно добијамо да је $\rho>1$, што је тачно.
Овим смо показали, да је $x < 1 $ и да се кругови ${k}_{1}$ и ${k}_{2}$ секу у тачкама $A$ и $B$ (Слика 3).

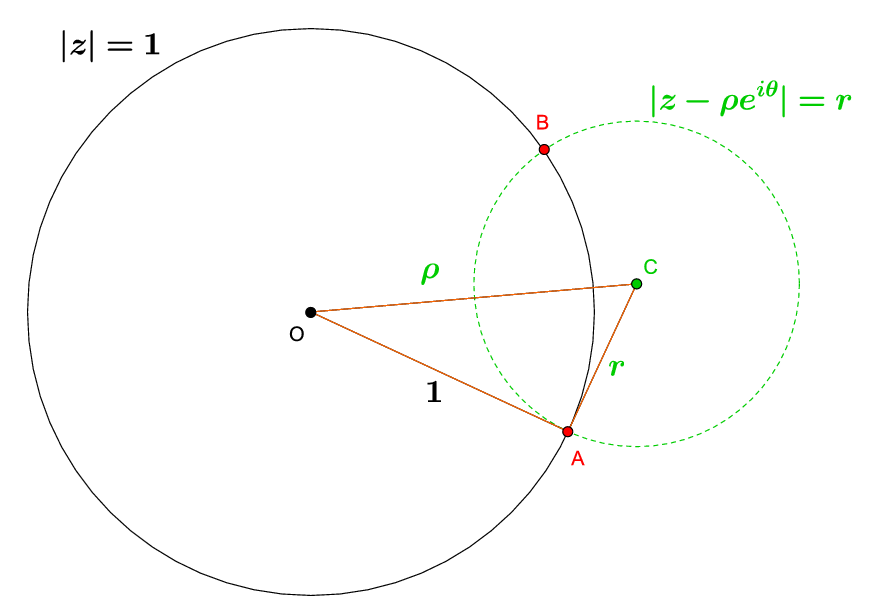Слика 3. Кругови $|z|=1$ и $|z-\rho {e}^{i\theta}|=r$ се секу у тачкама $A$ и $B$

Посматрајмо троугао $\triangle OAC$. Познате су нам дужине свих страница датог троугла и то је $OA=1$, $AC=r$ и $CO=\rho$. Међутим, како је $\displaystyle r=\sqrt{{\rho}^{2}-1}$, односно $\displaystyle {r}^{2}+{1}^{2}={\rho}^{2}$, на основу обрата Питагорине теореме следи да је троугао $\triangle OAC$ правоугли, тј. да је угао $\angle OAC$ прав. Овим смо доказали да су кругови ${k}_{1}$ и ${k}_{2}$ међусобно нормални.

Следећа теорема говори о нормалности уопштеног круга и круга $\{z\in \mathbb{C}: |z| < 1 \}$.

      Теорема: Уопштени круг $\{z\in \mathbb{C}: Ez\overline{z}+F\overline{z}+\overline{F}z+G=0, E,G\in \mathbb{R},F\in \mathbb{C},{|F|}^{2}-EG>0\}$ је нормалан на круг $\{z\in \mathbb{C}:|z|=1\}$ ако и само ако је $E=G$.

      Доказ: Разликоваћемо два случаја, када је $E=0$ и када је $E\neq 0$.
      У првом случају $(E= 0)$ уопштени круг је права. Права је нормална на круг ако и само ако садржи центар тог круга. У овом случају права је нормална на круг $\{z\in \mathbb{C}:|z|=1\}$ ако и само ако садржи тачку $0$, тј. ако и само ако је $\overline{F}\cdot 0+F\cdot \overline{0}+G=0$. Али како је $\overline{0}=0$, следи да је $\overline{F}\cdot 0+F\cdot \overline{0}+G=0$ ако и само ако је $G=0$.       У другом случају $(E\neq 0)$ посматрајмо произвољан круг $Ez\overline{z}+F\overline{z}+\overline{F}z+G=0$. нађимо прво центар и полупречник овако задатог круга. Како је $Ez\overline{z}+F\overline{z}+\overline{F}z+G=0$ и $E,G\in \mathbb{R}$ и $a+b\cdot i ,a,b\in \mathbb{R}$ можемо закључити следеће: $$Ez\overline{z}+F\overline{z}+\overline{F}z+G=0$$ $$\Leftrightarrow Ex^2+Ey^2+2ax+2by+G=0$$ $$\Leftrightarrow x^2+y^2+2\frac{a}{E}x+2\frac{b}{E}y+\frac{G}{E}=0$$ $$\Leftrightarrow \left(x+\frac{a}{E}\right)^2+\left(y+\frac{b}{E}\right)^2=\frac{a^2}{E^2}+\frac{b^2}{E^2}-\frac{G}{E}$$ $$\Leftrightarrow \left(x+\frac{a}{E}\right)^2+\left(y+\frac{b}{E}\right)^2=\frac{a^2+b^2}{E^2}-\frac{GE}{E^2}$$ $$\Leftrightarrow \left(x+\frac{a}{E}\right)^2+\left(y+\frac{b}{E}\right)^2=\frac{{|F|}^2-GE}{E^2}$$ Из овога можемо закључити да је $$\displaystyle {r}^{2}=\frac{{|F|}^{2}-EG}{{E}^{2}}.$$ Даљим сређивањем израза $\left(x+\frac{a}{E}\right)^2+\left(y+\frac{b}{E}\right)^2=\frac{{|F|}^2-GE}{E^2}$ можемо добити центар датог круга. $$\left(x+\frac{a}{E}\right)^2+\left(y+\frac{b}{E}\right)^2=\frac{{|F|}^2-GE}{E^2}$$ $$\Leftrightarrow \left(x+\frac{a}{E}\right)^2+\left(y+\frac{b}{E}\right)^2=r^2$$ $$\Leftrightarrow \sqrt{\left(x+\frac{a}{E}\right)^2+\left(y+\frac{b}{E}\right)^2}=r$$ $$\Leftrightarrow \left|\left(x+\frac{a}{E}\right)+\left(y+\frac{b}{E}\right)\cdot i\right|=r$$ $$\Leftrightarrow \left|\left(x+y\cdot i\right)+\left(\frac{a}{E}+\frac{b}{E}\cdot i\right)\right|=r$$ $$\Leftrightarrow \left|z+\frac{F}{E}\right|=r$$ Дакле, центар круга је $\displaystyle {z}_{0}=\rho{e}^{i\theta}=\displaystyle -\frac{F}{E}$. Односно $\displaystyle \rho=\left|-\frac{F}{E}\right|$. На основу леме имамо да ће ова два круга бити међусобно нормална ако и само ако је $\displaystyle r=\sqrt{{\rho}^{2}-1}$. Односно ако и само ако је $${r}^{2}={\rho}^{2}-1$$ $$\Leftrightarrow \frac{{|F|}^{2}-EG}{{E}^{2}}=\frac{{|F|}^{2}}{{E}^{2}}-1$$ $$\Leftrightarrow {|F|}^{2}-EG={|F|}^{2}-{E}^{2}$$ $$\Leftrightarrow -G=-E$$ $$\Leftrightarrow E=G.$$ Овим смо доказали теорему која даје услов нормалности уопштеног круга и круга $|z|=1$.

На следећем аплету можете видети како изгледа уопштени круг који је нормалан на круг $|z|=1$.

Ovo je Java Applet napravljen u GeoGebri sa www.geogebra.org - izgleda da nemate instaliranu Javu; molim otvorite www.java.com

Из наведеног можемо закључити следеће:

1. Ако је $E=0$ добијамо једначину $2ax+2by=0$, односно, гледано еуклидским очима, добијамо једначину праве која садржи координатни почетак.
2. Ако је $E\neq 0$ добијамо једначину $Ex^2+Ey^2+2ax+2by+E=0$ која, опет гледано еуклидским очима, представља једначину круга.

На основу свега наведеног моћемо закључити да из једначине уопштеног круга добијамо једначину праве у случају када је $E=0$, у супротном ($E\neq 0$) добијамо једначину круга.