Помоћни резултати из еуклидске геометрије »
Помоћни резултати из комплексне анализе »
Аксиоме хиперболичке геометрије равни »
Конструкција Поенкареовог диск модела »
Провера аксиома у Поенкареовом диск моделу »
Карактеристике хиперболичке равни у Поенкареовом диск моделу »
Примери »
„Визуелизација Поенкареовог диск модела коришћењем програмског пакета GeoGebra“
Марина Јовановић,
Универзитет у Београду, Математички факултет
Карактеристике хиперболичке равни
у Поенкареовом диск моделу
У овом делу уводимо појмове прамен $h-$правих и $h-$епицикл. У еуклидској геометрији равни за две дисјунктне праве кажемо да су паралелне. У хиперболичкој геометрији равни две дисјунктне праве могу бити паралелне и хиперпаралелне. Појмове паралелности и хиперпаралелности правих у хиперболичкој геометрији равни увешћемо на Поенкареовом диск моделу.
Две $h-$праве су међусобно паралелне ако имају један заједнички крај (Слика 1).
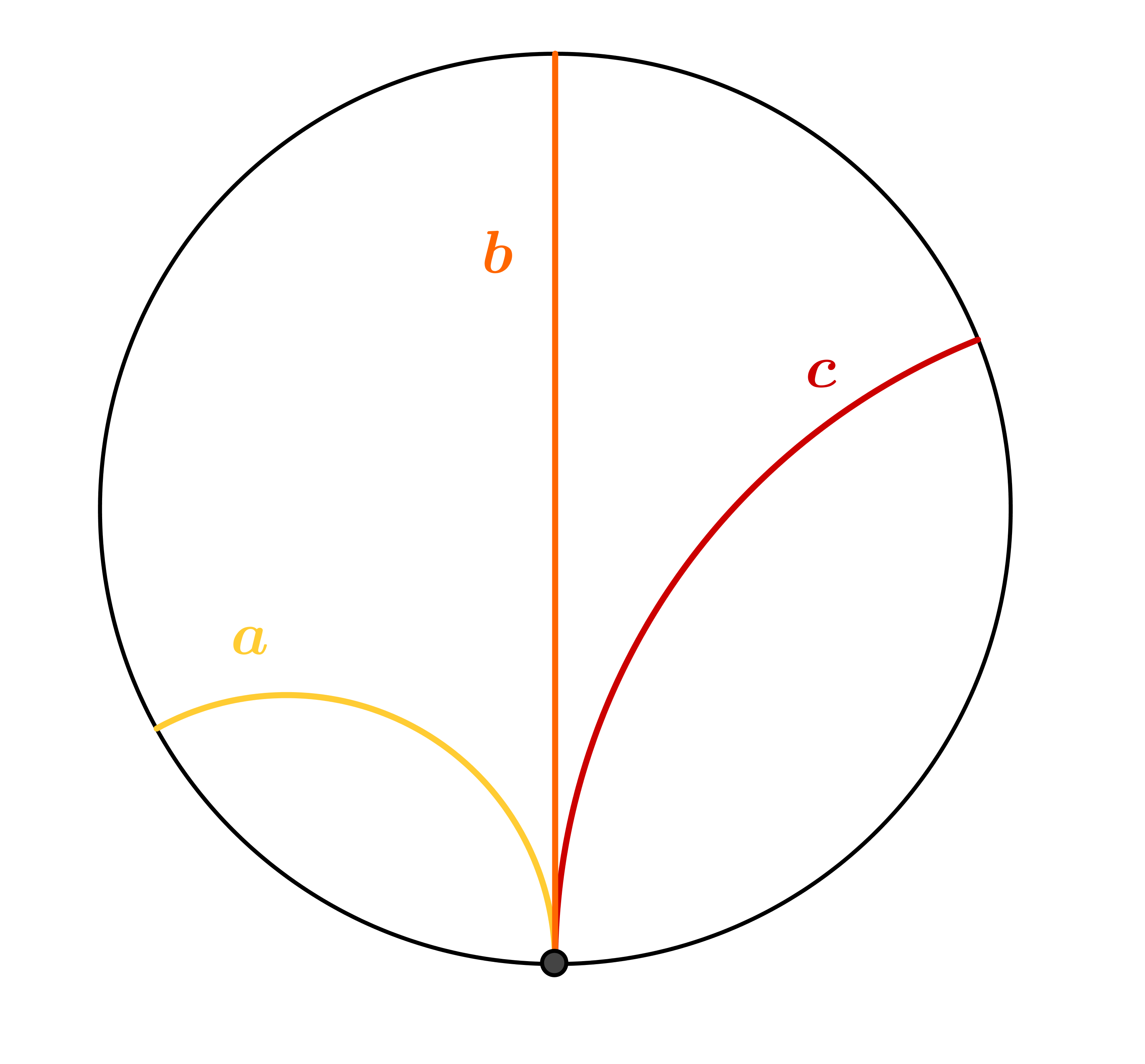 |
||
| Слика 1. Пример две паралелне $h-$праве |
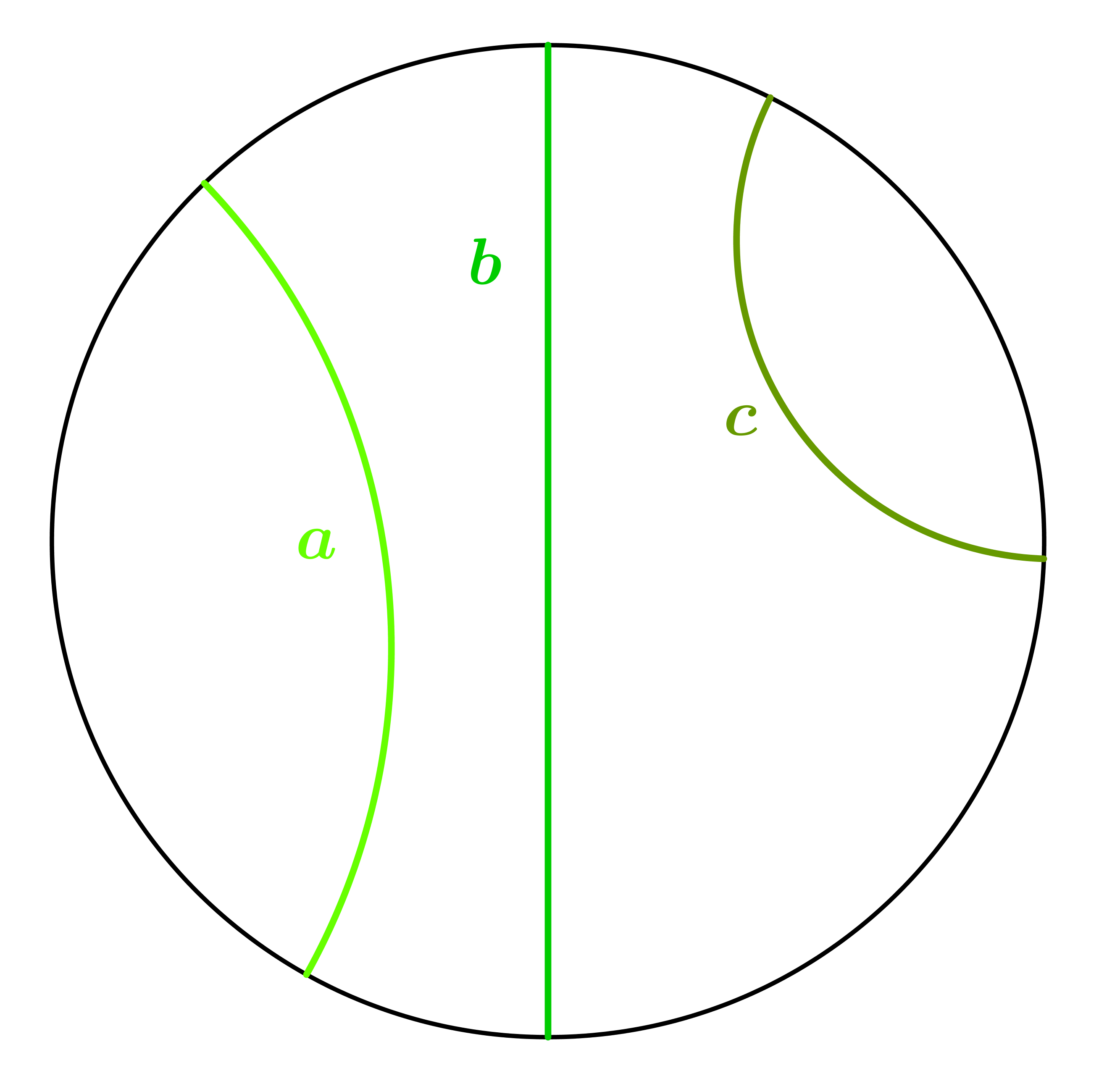
Две $h-$праве су међусобно хиперпаралелне ако су дисјунктне и немају заједнички крај (Слика 2).
 |
||
| Слика 2. Пример две хиперпаралелне $h-$праве |
Теорема: За две међусобно хиперпаралелне $h-$праве постоји јединствана $h-$права нормална на обе.
Даћемо визуелни доказ теореме.
Нека је $k$ апсолута и $a$ и $b$ две хиперпаралелне $h-$праве. Означимо са $O$ центар апсолуте.
Разликујемо два случаја:
Елиптички прамен $h-$правих је скуп свих $h-$правих које садрже неку $h-$тачку (Слика 3).
 |
||
| Слика 3. Пример елиптичког прамена $h-$правих |
Како кругови који садрже неку $h-$тачку садрже и њој инверзну тачку у односу на апсолуту (јер су нормални на апсолуту), све $h-$праве елиптичког прамена припадају круговима елиптичког прамена кругова.
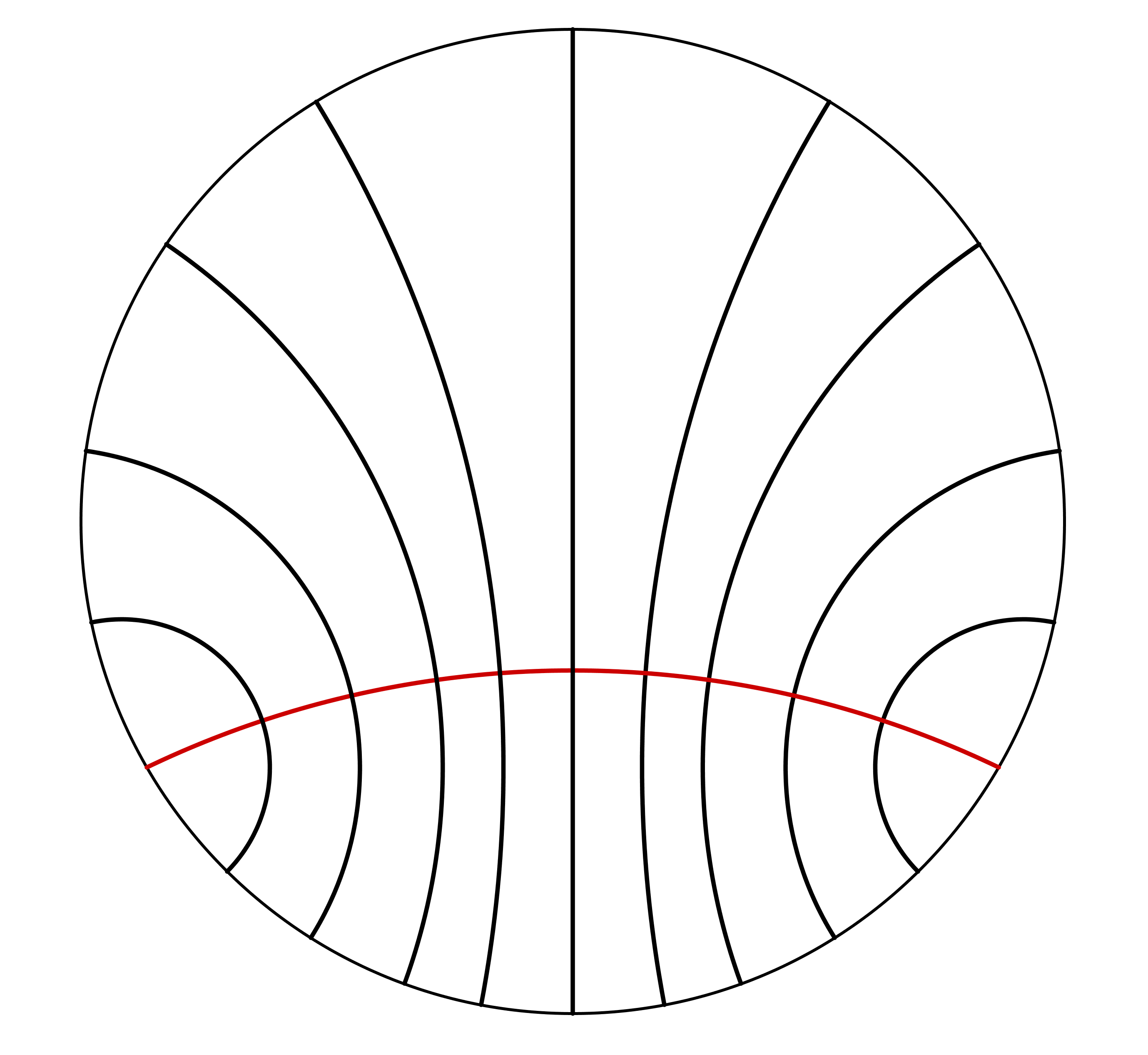
Хиперболички прамен $h-$правих је скуп свих $h-$правих које немају ни заједничку $h-$тачку ни заједнички крај (Слика 4).
 |
||
| Слика 4. Пример хиперболичког прамена $h-$правих |
Све $h-$праве хиперболичког прамена $h-$правих припадају хиперболичком прамену кругова.
Параболички прамен $h-$правих је скуп свих $h-$правих које имају један заједнички крај (Слика 5).
 |
||
| Слика 5. Пример параболичког прамена $h-$правих |
Центри кругова који садрже $h-$праве параболичког прамена $h-$правих припадају тангенти на апсолуту у заједничком крају датих $h-$правих. Отуда све $h-$праве параболичког прамена припадају круговима параболичког прамена кругова.
Нека је $\mathfrak{X}$ прамен $h-$правих (елиптички, хиперболички или параболички) и нека је $X$ произвољна $h-$тачка која не припада свим елементима прамена $\mathfrak{X}$. $h-$Епицикл одређен праменом $\mathfrak{X}$ и тачком $X$ је скуп $\left\{\mathcal{S}_x(X): x\in \mathfrak{X}\right\}$ (Са $\mathcal{S}_x$ обележавамо $h-$рефлексију хиперболичке равни чија је оса $h-$права $x$.), који обележавамо са $\mathcal{E}(\mathfrak{X},X)$.
Теорема: Сваки $h-$епицикл у Поенкареовом диск моделу је еуклидски круг или део еуклидског круга.
У зависности од врсте прамена $h-$правих разликујемо три врсте $h-$епицикала.
Нека је $\mathfrak{X}$ елиптички прамен $h-$правих и нека је $S$ заједничка $h-$тачка $h-$правих које припадају прамену $\mathfrak{X}$. Прамен $\mathfrak{X}$ тада обележавамо и са $\mathfrak{X}_S$. $h-$Епицикл $\mathcal{E}(\mathfrak{X}_S,X)$ називамо $h-$круг, $h-$тачку $S$ $h-$центар, а $h-$дуж $SX$ $h-$полупречник тог $h-$круга.
Може се показати да је $h-$круг скуп свих $h-$тачака $Y$ за које важи $SX{\cong}_{h}SY$.
У Поенкареовом диск моделу $h-$круг је еуклидски круг. Напоменимо још и да је $h-$центар $h-$круга једнак еуклидском центру одговарајућег еуклидског круга једино у случају када је то центар апсолуте.
На следећем аплету можете видети конструкцију $h-$круга. Како би се $h-$круг конструисао унесите координате тачке $X$.
Напомена:
Када се унесу координате тачке $X$, тачку $X$ могуће је померати и помоћу миша.
Нека је $\mathfrak{X}$ хиперболички прамен $h-$правих и нека је $s$ заједничка нормала $h-$правих које припадају прамену $\mathfrak{X}$. Прамен $\mathfrak{X}$ тада обележавамо и са $\mathfrak{X}_s$. $h-$Епицикл $\mathcal{E}(\mathfrak{X}_s,X)$ називамо $h-$еквидистанта, а $h-$праву $s$ основица $h-$еквидистанте. Означимо са $X'$ подножје нормале из $h-$тачке $X$ на $h-$правој $s$. $h-$Дуж $XX'$ називамо висина $h-$еквидистанте.
Може се показати да је $h-$еквидистанта скуп свих $h-$тачака $Y$ за које важи $XX'{\cong}_{h}YY'$, при чему је $Y'$ подножје нормале из $h-$тачке $Y$ на $h-$правој $s$.
У Поенкареовом диск моделу $h-$еквидистанта је лук еуклидског круга. Напоменимо још и да је основица $h-$еквидистанте нормална на апсолуту.
На следећем аплету можете видети конструкцију $h-$еквидистанте. Како би се $h-$еквидистанта конструисала унесите координате тачке $X$.
Напомена:
Када се унесу координате тачке $X$, тачку $X$ могуће је померати и помоћу миша.
Нека је $\mathfrak{X}$ параболички прамен $h-$правих и нека је $P$ заједнички крај $h-$правих којуе припадају прамену $\mathfrak{X}$. Прамен $\mathfrak{X}$ тада обележавамо и са $\mathfrak{X}_P$. $h-$Епицикл $\mathcal{E}(\mathfrak{X}_P,X)$ називамо $h-$орицикл.
У Поенкареовом диск моделу $h-$орицикл је еуклидски круг без једне тачке, заједничког краја $h-$правих одговарајућег прамена.
На следећем аплету можете видети конструкцију $h-$орицикла. Како би се $h-$орицикл конструисао унесите координате тачке $X$.
Напомена:
Када се унесу координате тачке $X$, тачку $X$ могуће је померати и помоћу миша.


