Uvod »
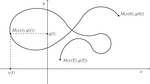
Kretanje u 2D »
Ojlerova formula »
Definisanje exp u $R^2$ »
Primer kretanja »
Definisanje exp u $R^3$ »
Određivanje Zorich mapp »
Ispitivanje Zorich mapp »
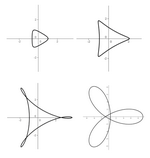
Vizuelizacija Zorich »
Zaključak »
Закључак:
Ojlerova formula se često koristi u raznim oblastima i primenama matematike. Formula daje vezu između funkcija iz na prvi pogled potpuno različitih klasa – vezu između eksponencijalne i trigonometrijskih funkcija. Otuda postoji potreba da se pomenuta veza suštinski razume i objasni.Fizička interpretacija Ojlerove formule i veza sa kretanjem u dve dimenzijidoprinosi prirodnom uvođenju i razumevanju formule. Ojlerova formula se može uvesti na različite načine ikoristeći različite metodičke pristupe. Povezivanje i izvođenje matematičkih rezultata baziranih na fizičkim pojavama i procesima ima važnu metodičku i motivacionu ulogu u nastavi. Sa druge stane napredak informacionih tehnologija i stvaranje uslova za vizuelizaciju pojedinih fizičkih pojava i matematičkih principa može doprineti potpunijem i kvalitetnijem objašnjenju formula sa konkretnom fizičkom i matematičkom pozadinom. Ideja je da se pronadju što bolji načini, metodi i tehnike za prezentovanje, uvođenje i objašnjavanje matematičkih sadržaja, motivisanih na geometrijsko-fizičkoj interpretaciji.
