Кретање у 2D:

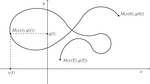
Posmatranje kretanja i samo kretanje predstavlja uobičajenu pojavu za većinu ljudi. Svakodnevno svesno ili nesvesno posmatramo i učestvujemo u različitim vrstama kretanja: kretanje od kuće do škole, kretanje Zemlje oko Sunca, Meseca oko Zemlje, kretanje svetlosti,vazduha, kretanje atoma i niz drugih primera. Značaj kretanja uvideli su i naučnici vekovima u nazad pokušavajući da opišu kretanje planeta, svetlosti, talasa, okeana i sl. Takođe i u srednjem veku kretanje je zauzimalo značajnu ulogu o čemu svedoči i prvi Njutnov zakon inercije. Kretanje možemo posmatrati u različitim dimenzijama, pa kretanje u jednoj dimenziji moglo bi se shvatiti kao kretanje po pravoj, kretanje u dve dimenziije kao kretanje u ravni i kretanje u tri dimenzije kao kretanje u prstoru. S obzirom da živimo u trodimenzionalnom prostoru najčešće se susrećemo sa kretanjem u tri dimenzije koje se često prestavlja u ravni tj u dve dimenzije. I ako ne deluje na prvi pogled kretanje u dve dimenzije je takođe prisutno i interesantno, pa su čak i prve video igrice zasnovane na dodimenzionalnom kretanju. Setimo se igrica za tetris i prve mobilne telefone, recimo igrica "Zmijice" koja ne prestavlja ništa drugo, nego kretanje tačke u ravni. Tema kretanja može biti sfera izučavanja mnogih nauka među kojima je i matematika. Zapravo kroz dalji tekst daćemo matematičko-mehaničku interpretaciju kretanja u dve dimenzije.

Promenu pozicije nekog objekta u odnosu na drugi referentni objekat nazivaćemo Motion objekta.Kretanje je potpuno određeno ako znamo vremenski interval tokom kojeg se kretanje odvija i poziciju objekta u odnosu na referentni objekat u svakom trenutku vremenskog intervala. Kretanje u dve dimenzije je kretanje u ravni. Ako u ravan uvedemo Dekartov koordinatni sistem, pozicija objekta koji se kreće je jedinstveno određena uređenim parom realnih brojeva. Pri tome tačku $(0,0)$ uzimamo za referentni objekat.

Preciznije, u ovom radu pretpostavljamo da kretanje počinje u trenutku $t=0$, a završava se i trenutku $t=T$, odnosno kretanje se odvija u vremenskom intervalu $[0,T]$. Poziciju objekta tokom kretanja definišemo sa position function $f: [0,T]→R^2$. Uvedimo oznaku $f(t)=(x(t),y(t))$. Otuda, ako sa M obeležimo objekat koji se kreće, njegova pozicija u trenutku $t∈[0,T]$ određena je sa $M(x(t),y(t))$. Takođe, pretpostavljamo da je funkcija $f$ neprekidno diferencijabilna.

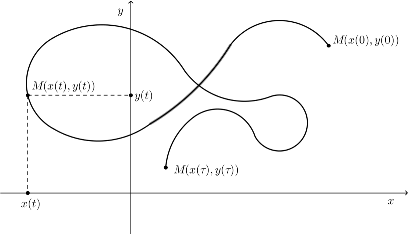
Razmotrimo, pređeni put objekta od početka kretanja do trenutka $t∈[0,T]$. U tom cilju, neka je $ 0=t_0 Pređeni put od trenutka $0$ do trenutka t definišemo kao funkciju $s:[0,T]→R$, određenu sa $$s(t)=\int\limits_0^t \sqrt{(x'(\tau))^2+(y'(\tau))^2 } d\tau$$ Funkciju s zovemo path function.

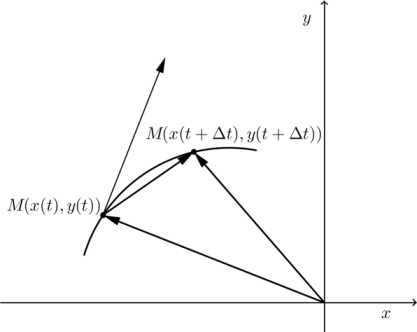
Pored pozicije objekta i pređenog puta važne veličine koje razmatramo u vezi kretanja su veličine velocity i speed. Velocity posmatramo kao vektorsku veličinu i opisujemo ga kao količnik promene pozicije objekta i proteklog vremena. Preciznije, definišemo srednji velocity na intervalu $[t,t+△t]$, na sledeći način

$$u_{avg} (t,t+\Delta t)={\frac{1}{t_{i+1}-t_i }((x(t+\Delta t)-x(t))(\overrightarrow{e_{1}})+(y(t+\Delta t)-y(t))(\overrightarrow{e_{2}} ))} \mbox{,}$$ gde su $(\overrightarrow{e_1} )=(1,0)$ i u $(\overrightarrow{e_2} ) =(0,1)$. I slično, trenutni velocity u trenutku $t$ definišemo na sledeći način $$ \begin{eqnarray*} u(t)= \lim_{\Delta t \to 0}{u_{avg} (t,t+\Delta t)} & = & \lim_{\Delta t \to 0} {\frac{1}{(\Delta t)} ((x(t+\Delta t)-x(t))(\overrightarrow{e_{1}})+(y(t+\Delta t)-y(t))(\overrightarrow{e_{2}} )} \\ & = & x'(t)\overrightarrow{e_1} +y' (t) \overrightarrow{e_2}. \end{eqnarray*}$$
Speed posmatramo kao skalarnu veličinu i opisujemo ga kao količnik pređenog puta i proteklog vremena. Preciznije, definišemo srednji speed na intervalu $[t,t+△t]$, na sledeći način $$\begin{eqnarray*} v_{avg} (t,t+\Delta t) & = & \frac{s(t+\Delta t)-s(t)}{\Delta t} \\ & = & \frac {\int\limits_0^{t+\Delta t} \sqrt{(x'(\tau))^2+(y'(\tau))^2 } d\tau-\int\limits_0^t \sqrt{(x'(\tau))^2+(y'(\tau))^2} d\tau}{\Delta t} \\ & = & \frac {\int\limits_t^{t+\Delta t} \sqrt{(x'(\tau))^2+(y'(\tau))^2 } d\tau}{\Delta t} \mbox{.} \end{eqnarray*} $$ I slično, trenutni speed u trenutku $t$definišemo na sledeći način $$v(t)=\lim_{\Delta t \to 0}{v_{avg} (t,t+\Delta t)}=\lim_{\Delta t \to 0}\frac{s(t+\Delta t)-s(t)}{(\Delta t)}=s'(t).$$ Primetimo da su veličine trenutni velocity i trenutni speed povezane jednakošću: $$v(t)=\parallel u(t)\parallel.$$ Zaista, kako je $s(t)=\int\limits_0^t {\sqrt{(x'(\tau))^2+(y'(\tau))^2 } d\tau }$, diferenciranjem dobijamo $s'(t)=\sqrt {(x'(t))^2+(y'(t))^2 }$. S druge strane, primetimo da je $\parallel u(t)\parallel =\sqrt{(x' (t))^2+(y' (t))^2 }$, odakle sledi jednakost (3). Napomenimo, da su velčine pređeni put, speed i velocity u potpunosti određene pozicijom objekta.