Uvod »
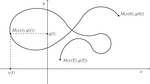
Kretanje u 2D »
Ojlerova formula »
Definisanje exp u $R^2$ »
Primer kretanja »
Definisanje exp u $R^3$ »
Određivanje Zorich mapp »
Ispitivanje Zorich mapp »
Vizuelizacija Zorich »
Zaključak »
Zorich mappig:
lema 1 (Prelazak sa Dekartovih na polarne koordinat) Neka tačka ima $(x_1, x_2)_dek$ koordinate, njene polarne koordinate u zavisnosti od znaka koordinata $x_1$ i $x_2$ su: $$(x_1, x_2)_{dek} \rightarrow \left \{ \begin{array}{ll} (\sqrt{x_1 ^2+x_2 ^2}, \arctan{\frac{x_2}{x_1}})_{pol}&x_1 > 0 , x_2 > 0\\ (\sqrt{x_1 ^2+x_2 ^2},\pi + \arctan{\frac{x_2}{x_1}})_{pol}& x_1 < 0 , x_2 < 0\\ (\sqrt{x_1 ^2+x_2 ^2},\pi + \arctan{\frac{x_2}{x_1}})_{pol}& x_1 < 0 , x_2 > 0 \\ (\sqrt{x_1 ^2+x_2 ^2},2\pi + \arctan{\frac{x_2}{x_1}})_{pol}& x_1 > 0 , x_2 < 0 \end{array} \right . $$Strečing kvadrata na krug
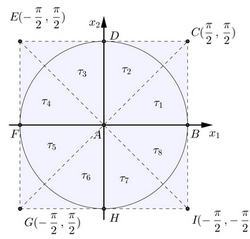
Ravan $(x_1, x_2)$ podelimo na jednake kvadrate, pokušavamo da presikamo kvadrat $[-\frac{\pi}{2}, \frac{3\pi}{2}]\verb"x"[-\frac{\pi}{2},\frac{3\pi}{2}]$ koji će biti pogodan za popločavanje čitave ravni, tako što prvo preslikavamo \v cetvrtinu tog kvadrata $[-\frac{\pi}{2}, \frac{\pi}{2}]\verb"x"[-\frac{\pi}{2},\frac{\pi}{2}]$ u krug. Odnosno izvršimo streching tog kvadrata na krug.
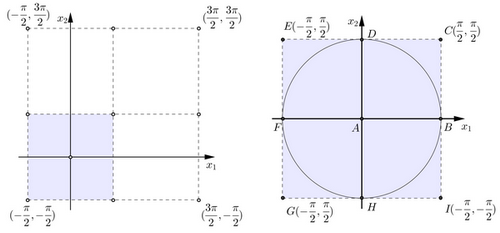
Zbog prelaska na polarne koordinate i osobina funkcije $\arctan$, da bismo odredili preslikavanje 'streching' moraćemo da posmatramo $8$ slučajeva u zavisnosti položaja tačke koju preslikavamo odnosno znaka koordinata $x_1$ i $x_2$ i znaka funkcije $\arctan\frac{x_1}{x_2}$.
(1) Razmotrimo slučaj kada je $x_1>0, x_2>0$, odnosno posmatrajmo prvu osminu kvadrata,
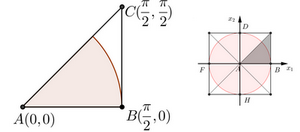
Obeležimo sa $\Phi$ funkciju koja trougao slika na osminu odgovarajućeg kruga. Tada je $$(\rho, \varphi)_{pol}\rightarrow(\rho\cos{\varphi},\varphi)_{pol} .$$ Koristeći lemu dobijamo: $$\Big(\sqrt{x_1 ^2+x_2 ^2}, \arctan{\frac{x_2}{x_1}}\Big)_{pol}\rightarrow\Big(\sqrt{x_1 ^2+x_2 ^2} \cdot \cos(\arctan{\frac{x_2}{x_1}}), \arctan{\frac{x_2}{x_1}}\Big)_{pol}.$$ Kako je $\arctan\frac{x_2}{x_1} \in (0,\frac{\pi}{2})$, tada \begin{eqnarray} \cos(\arctan\frac{x_2}{x_1})&=&\frac{1}{\sqrt{1+\tan^2(\arctan\frac{x_2}{x_1})}}\nonumber \\ &=&\frac{1}{\sqrt{1+(\frac{x_2}{x_1})^2}} \nonumber \\ &=&\frac{x_1}{\sqrt{x_1 ^2 + x_2 ^2}}. \nonumber \end{eqnarray} Pa preslikavanje ima konačan oblik $$\Big(\sqrt{x_1 ^2+x_2 ^2}, \arctan{\frac{x_2}{x_1}}\Big)_{pol}\rightarrow\Big(x_1, \arctan{\frac{x_2}{x_1}}\Big)_{pol}.$$ Analogno se uradi i za ostalih 7 slučajeva i preslikavanje streching na kvadratu koji smo ispitivali u zavisnosti od izabranog trougla je:
1)$ \left(\sqrt{x_1 ^2+x_2 ^2}, \arctan{\frac{x_2}{x_1}} \right)_{pol}\rightarrow \left(x_1, \arctan{\frac{x_2}{x_1}} \right)_{pol}, (x_1,x_2) \in \tau _1$ 2)$ \left(\sqrt{x_1 ^2+x_2 ^2}, \arctan{\frac{x_2}{x_1}} \right)_{pol}\rightarrow \left(x_2, \arctan{\frac{x_2}{x_1}} \right)_{pol}, (x_1,x_2) \in \tau _2$ 3)$ \left(\sqrt{x_1 ^2+x_2 ^2}, \pi + \arctan{\frac{x_2}{x_1}} \right)_{pol}\rightarrow \left(x_2,\pi + \arctan{\frac{x_2}{x_1}} \right)_{pol}, (x_1,x_2) \in \tau _3$ 4)$ \left(\sqrt{x_1 ^2+x_2 ^2}, \pi + \arctan{\frac{x_2}{x_1}} \right)_{pol}\rightarrow \left(-x_1,\pi + \arctan{\frac{x_2}{x_1}} \right)_{pol}, (x_1,x_2) \in \tau _4$ 5)$ \left(\sqrt{x_1 ^2+x_2 ^2}, \pi + \arctan{\frac{x_2}{x_1}} \right)_{pol}\rightarrow \left(-x_1,\pi + \arctan{\frac{x_2}{x_1}} \right)_{pol}, ( x_1,x_2) \in \tau _5$ 6)$ \left(\sqrt{x_1 ^2+x_2 ^2}, \pi + \arctan{\frac{x_2}{x_1}} \right)_{pol}\rightarrow \left(-x_2,\pi + \arctan{\frac{x_2}{x_1}} \right)_{pol}, (x_1,x_2) \in \tau _6$ 7)$ \left(\sqrt{x_1 ^2+x_2 ^2}, 2\pi +\arctan{\frac{x_2}{x_1}} \right)_{pol}\rightarrow \left(-x_2,2\pi +\arctan{\frac{x_2}{x_1}} \right)_{pol}, ( x_1,x_2) \in \tau _7$ 8)$ \left(\sqrt{x_1 ^2+x_2 ^2},2\pi + \arctan{\frac{x_2}{x_1}} \right)_{pol}\rightarrow\left(x_1, 2\pi+ \arctan{\frac{x_2}{x_1}} \right)_{pol}, (x_1,x_2) \in \tau _8$
Zorich mapping, preslikavanje diska na sferu i prelazak na Dekartove koordinate
Posmatrajmo tacke iz već definisanih trouglova $\tau_1 - \tau_8$ primenimo preslikavanja $C_D$ - promena koordinata primenom leme \ref{L1}, zatim preslikavanje $\Phi$ koje preslikava izabrani trougao na kružni isečak, zatim preslikavanje $\Psi$ dato sa $\Psi(\rho, \phi , x_3)_{cil}=(e^{x_3}, \phi, \rho)_{sfe}$ i na kraju $D_S$ promenimo koordinte u Dekrtove koristeći lemu \ref{L2}. $$Z=D_S \circ \Psi \circ \Phi \circ C_S $$

1) $\left(x_1, x_2, x_3\right) \in \tau_1 \times R$
$\left( x_1, x_2, x_3\right) _{dek}\rightarrow \left(\sqrt{x_1 ^2 + x_2 ^2}, \arctan{\frac{x_2}{x_1}},x_3\right)_{cil} $ $\rightarrow \left( x_1, \arctan{\frac{x_2}{x_1}},x_3\right)_{cil} \rightarrow \left( e^{x_3}, \arctan{\frac{x_2}{x_1}},x_1\right)_{sfe} $ $\rightarrow \left( e^{x_3}\cos\left(\arctan{\frac{x_2}{x_1}}\right)\sin x_1, e^{x_3}\sin\left(\arctan{\frac{x_2}{x_1}}\right)\sin x_1 , e^{x_3}\cos x_1\right)_{dek} $ $$\cos\left(\arctan{\frac{x_2}{x_1}}\right)=\frac{x_1}{\sqrt{x_1 ^2 +x_2 ^2}}$$ $$\sin\left(\arctan{\frac{x_2}{x_1}}\right)=\frac{x_2}{\sqrt{x_1 ^2 +x_2 ^2}}$$ Pa preslikavanje tačke koja pripada trouglu $\tau_1$ izgleda: $$\left(x_1, x_2, x_3\right)_{dek} \rightarrow \left( e^{x_3} \frac{x_1}{\sqrt{x_1 ^2 +x_2 ^2}} \sin x_1 , e^{x_3}\frac{x_2}{\sqrt{x_1 ^2 +x_2 ^2}}\sin x_1 , e^{x_3}\cos x_1\right)_{dek} $$ I slično za još ostalih 7 slučajeva.
Sisteamtizacija
$$ \left(x_1, x_2, x_3\right)_{dek} \rightarrow \left \{ \begin{array}{ll} \left( e^{x_3} \frac{x_1}{\sqrt{x_1 ^2 +x_2 ^2}} \sin x_1 , e^{x_3}\frac{x_2}{\sqrt{x_1 ^2 +x_2 ^2}}\sin x_1 , e^{x_3}\cos x_1\right)_{dek} & \left(x_1, x_2, x_3\right) \in (\tau_1 \cup \tau_8) \times R\\ \left( e^{x_3} \frac{x_1}{\sqrt{x_1 ^2 +x_2 ^2}} \sin x_2 , e^{x_3}\frac{x_2}{\sqrt{x_1 ^2 +x_2 ^2}}\sin x_2 , e^{x_3}\cos x_2\right)_{dek} & \left(x_1, x_2, x_3\right) \in (\tau_2 \cup \tau_3) \times R\\ \left(- e^{x_3} \frac{x_1}{\sqrt{x_1 ^2 +x_2 ^2}} \sin x_1 ,- e^{x_3}\frac{x_2}{\sqrt{x_1 ^2 +x_2 ^2}}\sin x_1 , e^{x_3}\cos x_1\right)_{dek} & \left(x_1, x_2, x_3\right) \in (\tau_4 \cup \tau_5) \times R\\ \left(- e^{x_3} \frac{x_1}{\sqrt{x_1 ^2 +x_2 ^2}} \sin x_2 ,- e^{x_3}\frac{x_2}{\sqrt{x_1 ^2 +x_2 ^2}}\sin x_2 , e^{x_3}\cos x_2\right)_{dek} & \left(x_1, x_2, x_3\right) \in (\tau_6 \cup \tau_7) \times R\\ \end{array} \right . $$
