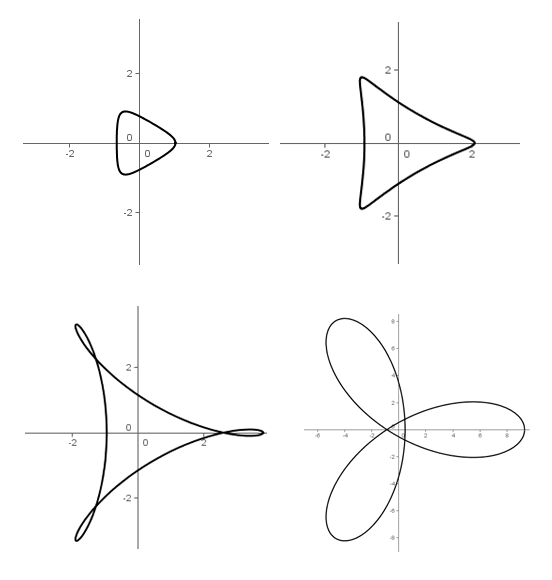
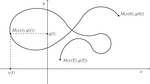
Primer kretanja:

Primer 1. Neka je $r\in(0,3]$ i neka je kretanje objekta $M $ u dve dimenzije zadato sa position function$ f_r:[0,2\pi]\rightarrow \mathbb{R}^2$, pri čemu je $f_r (t)=(r^2 \cos {2t}+2r \cos {t} ,r^2 \sin {2t}-2r \sin {t} )$ Tada je path function $s_r:[0,2\pi]\rightarrow \mathbb{R}$ određena sa $$s_r (t)=\int\limits_0^t\sqrt{(-2r^2 \sin 2\tau-2r \sin \tau )^2+(2r^2 \cos 2\tau-2r \cos \tau )^2 }d\tau.$$ Odnosno, nakon sređivanja $$s_r (t)=2r\int \limits_0^t \sqrt {(r^2-2r \cos 3\tau +1)} d\tau.$$ Trenutni velocity $u_r :[0,2\pi]\rightarrow \mathbb{R}^2 $je određen sa $$u_r (t)=(-2r^2 \sin {2t}-2r \sin {t},2r^2 \cos {2\tau}-2r \cos {\tau}).$$ Dok je trenutni speed $v_r:[0,2\pi]\rightarrow \mathbb{R} $ određen sa $$v_r (t)=2r\sqrt {(r^2-2r \cos 3\tau+1 ).}$$