Uvod »
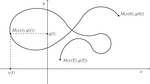
Kretanje u 2D »
Ojlerova formula »
Definisanje exp u $R^2$ »
Primer kretanja »
Definisanje exp u $R^3$ »
Određivanje Zorich mapp »
Ispitivanje Zorich mapp »
Vizuelizacija Zorich »
Zaključak »
Дефинисање exp у $R^3$:
Navedeni način uvođenja eksponencijalne funkcije $(R^2 \rightarrow R^2 )$, kao funkcije koja zadovoljava uslove $(1-5)$, može poslužiti kao motiv za uvođenje eksponencijalne funkcije $ (R^3 \rightarrow R^3 )$. Dokažimo da postoji funkcija $F:R^3 \rightarrow R^3 $, koja zadovoljava uslove:$1^\circ F(x,y,0)=(e^x\cos y,e^x\sin y,0 )=e^x(\cos y, \sin y, 0)$
$2^\circ F(x,y,t)=(e^x\cos y,e^x\sin y, e^xT_{33}(t))=e^x(\cos y T_{31}(t), \sin y T_{32}(t), T_{33}(t))$
$3^\circ <(\cos y T_{31}(t), \sin y T_{32}(t), T_{33}(t)),(\cos y T_{31}^{'}(t), \sin y T_{32}^{'}(t), T_{33}^{'}(t))>=0$
$4^\circ < (\cos y T_{31}^{'}(t), \sin y T_{32}^{'}(t), T_{33}^{'}(t)),(\cos y T_{31}^{"}(t), \sin y T_{32}^{"}(t), T_{33}^{"}(t))>=0$
$5^\circ (\cos y T_{31}^{'}(0), \sin y T_{32}^{'}(0), T_{33}^{'}(0))=(0,0, 1)$
Dokaz: Iz $1^\circ$ i $2^\circ$ sledi: \begin{equation} T_{31}(0)=1 , T_{32}(0)=1 , T_{33}(0)=0 \end{equation}
Iz $5^\circ$ sledi : \begin{equation} T_{31}^{'}(0)=1 ,
T_{32}^{'}(0)=1 ,
T_{33}^{'}(0)=0 \end{equation}
Iz $3^\circ$ sledi:$$\cos ^{2}y T_{31}(t)(T_{31})^{'}(t)+\sin ^{2}y T_{32}(t)(T_{32})^{'}(t)+T_{33}(t)(T_{33})^{'}(t)=0 /\int dt$$ $$\frac{1}{2}\cos ^{2}y (T_{31}(t))^{2}+\frac{1}{2}\sin ^{2}y (T_{31}(t))^{2}+\frac{1}{2}(T_{33}(t))^{2}=C(y)$$ Dobijamo : $$\frac{1}{2}\cos^{2}y+\frac{1}{2}\sin^{2}y=C(y)$$ Odnosno, $$C(y)=\frac{1}{2},$$ odatle \begin{equation} \cos ^{2}y (T_{31}(t))^{2}+\sin ^{2}y (T_{31}(t))^{2}+(T_{33}(t))^{2}=1 \end{equation} Formula važi za svako $(y,t)\in R^{2}$. Otuda ako je $y=0$ \begin{equation} (T_{31}(t))^{2}+(T_{33}(t))^{2}=1 \end{equation} odnosno ako je $y=\frac{\pi}{2}$ \begin{equation} (T_{32}(t))^{2}+(T_{33}(t))^{2}=1, \end{equation} Iz gornje 2 jednačine dobijamo $$(T_{31}(t))^{2}=(T_{32}(t))^{2}.$$ Kako smo pretpostavili da su $T_{31}, T_{32}, T_{33}\in C^{1}(R)$ sledi da je $T_{31}(t)=T_{32}(t)$ ili $T_{31}(t)=-T_{32}(t)$. Međutim kako je $T_{31}(0)=1$ i $T_{32}(0)=1$ zaključujemo da je \begin{equation} T_{31}(t)=T_{32}(t) \end{equation} Na osnovu prethodnog sledi da postoji funkcija $\phi:R \longrightarrow R $, takve da je \begin{equation} T_{31}(t)=\cos \phi (t) , T_{32}(t)=\cos \phi (t) , T_{33}(t)=\sin \phi (t) \end{equation} Preostaje još da bliže odredimo funkciju $\phi$. \begin{equation} T'_{31}(t)=-\phi'(t) \sin \phi (t) , T'_{32}(t)=-\phi'(t)\sin \phi (t) , T'_{33}(t)=\phi'(t)\cos \phi (t) \end{equation} Pa važi: $$\cos\phi(0)=1$$ $$\sin \phi(0)=0$$ $$-\phi'(t)\sin \phi (0)=0$$ $$\phi'(t)\cos \phi (0)=1$$ tj. $\phi(0)=2k\pi$ za neko $k \in Z$ i $\phi^{'}(0)=1.$
Iz $(4^\circ )$ sledi $$\cos ^{2}y T_{31}^{'}(t)(T_{31})^{"}(t)+\sin ^{2}y T_{32}^{'}(t)(T_{32})^{"}(t)+T_{33}^{'}(t)(T_{33})^{"}(t)=0. $$ Odnosno $$\frac{1}{2}\cos ^{2}y (T_{31}^{'}(t))^{2}+\frac{1}{2}\sin ^{2} y (T_{31}^{'}(t))^{2}+\frac{1}{2}(T_{33}^{'}(t))^{2}=C(y)$$ Kako je $T_{31}^{'}(0)=0$, $T_{32}^{'}(0)=0$, $T_{33}^{'}(0)=1$. Dobijamo $C(y)=\frac{1}{2}$, odnosno važi \begin{equation} \cos ^{2}y (T_{31}^{'}(t))^{2}+\sin ^{2}y (T_{32}^{'}(t))^{2}+(T_{33}^{'}(t))^{2}=1 \label {I} \end{equation} Zamenom dobijamo : $$(\phi(t)^{'})^{2}\cos ^{2}y\sin^{2}\phi(t)+(\phi(t)^{'})^{2}\sin ^{2}y\sin^{2}\phi(t)+(\phi(t)^{'})^{2} \cos^{2}\phi(t)=1$$ $$(\phi(t)^{'})^{2}\sin ^{2}\phi(t)+(\phi(t)^{'})^{2} \cos^{2}\phi(t)=1$$ $$(\phi(t)^{'})^{2}=1$$ Kako je $\phi ^{'}$ neprekidna i $\phi ^{'}(0)=1$
Dobijamo $$\phi ^{'}(t)=1$$ odnosno $$\phi(t)=t+C$$ odnosno kako je $\phi(0)=2k\pi$, za neko $k\in Z$ sledi $C=2k\pi$, za to isto $k\in Z.$ Konačno $$\phi(t)=t+2k\pi$$ Odnosno $$T_{31}(t)=\cos(t+2k\pi)=\cos t$$ $$T_{32}(t)=\cos(t+2k\pi)=\cos t$$ $$T_{33}(t)=\sin(t+2k\pi)=\sin t$$ Konačno funkciju $exp:\mathbf{R}^3\rightarrow\mathbf{R}^3$ definišemo na sledeći način: $$exp(x,y,z)=(e^x\cos{y}\cos{z}, e^x\sin{y}\cos{z}, e^x\sin{z}).$$
