Uvod »
Kretanje u 2D »
Ojlerova formula »
Definisanje exp u $R^2$ »
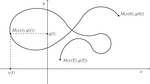
Primer kretanja »
Definisanje exp u $R^3$ »
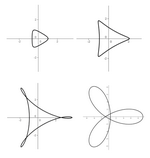
Određivanje Zorich mapp »
Ispitivanje Zorich mapp »
Vizuelizacija Zorich »
Zaključak »
проф. др Миодраг Матељевић,
Марек Светлик,
Марија Радојичић,
Славиша Радовић
Универзитет у Београду, Математички факултет
„Ojlerova formula, uopštenje eksponencijalne funkcije i vizuelni prikaz Zorich mapping“
Увод:
U svetu matematike pojedine formule plene pažnju svojom složenošću, svrsishodnošću, očiglednošću, jednostavnošću, a neke pak lepotom. Prema mišljenju mnogih matematičara jedna od najlepših matematičkih formula ikada izvedena je Ojlerov identitet $e^{iπ}+1=0$. Matematičari argumentovano objašnjavaju lepotu ove formule ističući da ona povezuje pet možda najznačajnijih matematičkih konstanti. Broj $0$ kao neutral za sabiranje, broj $1$ kao neutral za množenje, brojeve $π$ i $e$ kao važne matematičke konstante kao i imaginarnu jedinicu $i$. Navedeni identitet koji se jednostavno izvodi iz Ojlerove formule $ e^{it}=cost+isint$, izaziva pažnju velikog broja matematičara.
Ojlerova formula se veoma često koristi u raznim granama matematike, pa je svoje mesto našla u mnogim srednjoškolskim i univerzitetskim udžbenicima matematike. Učenici vrlo brzo ovladaju tehnikama korišćenja date formule, međutim problem se javlja prilikom uvođenja pomenute formule i suštinskog razumevanja iste. Da to nije samo trenutni problem, već da su se i edukatori godinama unazad pitali kako prirodno uvesti Ojlerovu formulu svedoče reči Harvardskog profesora Benjamin Pierce (19. vek), nakon dokazivanja Ojlerove formule: ”Gentlemen, that is surely true, it is absolutely paradoxical; we cannot understand it, and we don't know what it means. But we have proved it, and therefore we know it must be the truth."
U ovim materijalima dajemo jedan od mogućih načina uvođenja Ojlerove formule kao i mehaničku interpretaciju formule zasnovanu na kretanju tačke u ravni. Motivisani pomenutim kretanjem uvodimo eksponencijalnu funkciju u dve dimenzije $exp: {R}^2 \rightarrow {R}^2$. Prirodno, postavlja se pitanje kako definisati eksponencijalnu funkciju u tri i više dimenzija $exp: {R}^3 \rightarrow {R}^3$, što nas dovodi do Zorich mappinga.
