Ojlerova formula

Poznato je da se funkcija $f: R \rightarrow R$, data sa $f(x)=e^x$ može proširiti na skup $C$. Ispostavi se da za kompleksan broj $z=x+iy$ važi $e^z=e^x \cos y+ie^x \sin y$. Specijalno, ako je $z$ čisto imaginaran broj, tj. ako je $x=0$, dobijamo $$e^{iy}=\cos y+i \sin y\mbox{.}$$ Poslednja jednakost je možda neočekivana. Naime, na prvi pogled nije jasno zašto postoji jednostavna veza između eksponencijalne funkcije i trigonometrijskih funkcija. U ovoj sekciji koristeći kretanje u ravni dajemo prirodno objašnjenje ove veze. Neka je $t$ proizvoljan realan broj i pretpostavimo da je jedino poznato da $e^{it}$ pripada skupu kompleksnih brojeva. Dakle, možemo posmatrati funkciju $g:R→C$, definisanu sa $g(t)=e^{it}$. Formalnim diferenciranjem funkcije $g$ (uzimajući u obzir da je $i$ konstanta) dobijamo $g'(t)=ie^{it}$. Otuda, za svako $t \in \mathbb{R}$ važi $g'(t)=ig(t)$ Takođe, primetimo da je \begin{equation}\label{modul_izvoda} |g' (t)|=|ig(t) |=|i||g(t)|=|g(t)|\mbox{.} \end{equation} Ako pretpostavimo da je funkcija $g$ neprekidno diferencijabilna na intervalu $[0,2\pi ]$, restrikciju funkcije $g$ na interval $[0,2\pi ]$ možemo posmatrati kao position function kretanja nekog objekta $M$. Koristeći definicije koje smo uveli za kretanje u kompleksnoj ravni i uvodeći oznake $z=g|_{[0,2\pi ]}$, $x=Re z$ i $y=Im z$ dobijamo sledeće parametre posmatranog kretanja. Path function je određen jednakošću $s(t)=\int _0^t |ie^{i\tau } | d\tau $ $=\int _0^t|i||e^{i\tau } | d\tau $ $=\int _0^t|e^{i\tau } | d\tau .$ Trenutni velocity je određen sa $u(t)= ie^{it}$,dok je trenutni speed određen sa $v(t)=|ie^{it} |=|i||e^{it} |=|e^{it} |.$ Na osnovu osobine množenja kompleksnog broja imaginarnom jedinicom $i$ zaključujemo da je, u svakom trenutku, ugao između vektora pozicije objekta $M$ i trenutnog velocity objekta $M$ konstantan i jednak $\frac{\pi}{2}$ .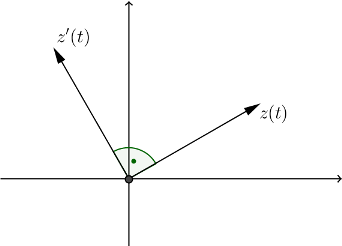

Integraljenjem jednakosti $\langle(x(t),y(t)),(x'(t),y'(t))\rangle=0\mbox{,}$ dobijamo da za svako $t\in[0,2\pi ]$ važi $$\int x(t) x' (t)dt+\int y(t) y' (t)dt=C\mbox{,}$$ tj. $$\frac{(x(t))^2}{2}+\frac{(y(t))^2}{2}=C\mbox{,}$$ pri čemu je $C$ realna konstanta. Kako je $z(0)=1$, dobijamo da je $x(0)=1$ i $y(0)=0$. Otuda dobijamo da je $C=\frac{1}{2}$. Konačno, za svako $t\in [0,2\pi ]$ važi $$(x(t))^2+(y(t))^2=1\mbox{,}$$ tj. \begin{equation}\label{z_krug} |z(t)|=|e^{it}|=1\mbox{.} \end{equation} Iz jednakosti $(x(t))^2+(y(t))^2=1\mbox{,}$ sledi da za svako $t\in[0,2\pi]$ tačka $z(t)$ pripada kružnici sa centrom $0$ i poluprečnikom $1$ (slika funkcije $z$ je sadržana u jediničnoj kružnici). Koristeći definicije funkcija kosinus i sinus pomoću trigonometrijskog kruga, dobijamo da postoji funkcija $\phi:[0,2\pi ]\rightarrow R$, takva da za svako $t\in[0,2\pi ]$, važi $$x(t)=\cos \phi(t) $$ i $$y(t)=\sin \phi(t) .$$ Odnosno, \begin{equation}\label{t_krug} z(t)=\cos \phi(t) +i \sin \phi(t)\mbox{.} \end{equation}

Sa druge strane, kako je $$z(t)=e^{it},$$ sledi \begin{equation}\label{t_krug1} e^{it}=\cos \phi(t)+i \sin \phi(t)\mbox{.} \end{equation} Odredimo preciznije funkciju $\phi$. U tom cilju pretpostavimo da je funkcija $\phi$ neprekidno diferencijabilna. Koristeći da je $z'(t)=iz(t)$, dobijamo da za svako $t\in[0,2\pi]$ , važi $$(-\sin \phi (t) ) \phi ' (t)+i(\cos \phi (t) ) \phi ' (t)=i(\cos \phi (t)+i \sin \phi (t) ),$$ odnosno \begin{equation}\label{phi_prim} (-\sin \phi (t) ) \phi ' (t)= -\sin \phi (t)\quad \mbox{ i } \quad (\cos \phi (t) ) \phi' (t)=\cos \phi(t)\mbox{.} \end{equation} Imajući u vidu da je za svako $t\in[0,2\pi ]$, bar jedan od brojeva$ \cos \phi(t)$ i $\sin \phi(t)$ različit od $0$, dobijamo \begin{equation}\label{phi_prim1} \phi '(t)=1\mbox{.} \end{equation} Konačno, rešavanjem diferencijalne jednačine dobijamo da za svako $t\in[0,2\pi]$ važi \begin{equation}\label{krajnja} e^{it}=\cos t+i \sin t\mbox{,} \end{equation} tj. $$z(t)=\cos t+i \sin t.$$ Kako funkciju $z$ interpretiramo kao position function kretanja objekta $M$, zaključujemo da je trenutni velocity objekta $M$ $u(t)=-\sin t+i \cos t.$ Specijalno, kada je $t=\pi$, imamo $$e^{i\pi }=-1\mbox{,}$$ odnosno, $$e^{i\pi} +1=0\mbox{.}$$