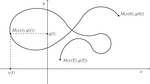
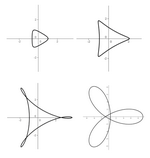
Дефинисање exp у $R^2$:
Pretpostavimo sada da neka funkcija $F : {R}^2 \rightarrow {R}^2$ zadovoljava $1^\circ - 5^\circ$
$$1^\circ F(x,0)=(e^x, 0)=e^x (1,0)$$
$$2^\circ F(x,t)=e^x(1\cdot T_{21}(t), T_{22}(t))$$
$$3^\circ <(1\cdot T_{21}(t),T_{21}(t)), ( (1 \cdot T_{21}(t))',(T_{21}(t))')>=0$$
$$4^\circ <((1 \cdot T_{21}(t))',(T_{21}(t))'), ( (1 \cdot T_{21}(t))'',(T_{21}(t))'')>=0$$
$$5^\circ (1\cdot T'_{21}(0), T'_{22}(0))=(0,1)$$
Pokušajmo da odredimo funkciju $F$. Iz $1^\circ$ i $2^\circ$ sledi
$$T_{21}(0)=1$$
$$T_{22}(0)=0\label{*}$$
Iz $3^\circ$ sledi
$$T'_21(0)=0$$
$$T'_22(0)=1\label{**}$$
Iz $3^\circ$ sledi
$$T_{21}(t)\cdot T'_{21}(t) + T_{22}(t)\cdot T'_{22}(t)=0 / \int$$
$$\frac{1}{2}(T_{21}(t))^2 + \frac{1}{2}(T_{22}(t))^2= C$$
kako to važi za svako $t$, neka je onda $t=0$. Dobijamo
$$\frac{1}{2}1^2 + \frac{1}{2} 0^2=C$$
$$C=\frac{1}{2}.$$
pa važi
\begin{equation}
(T_{21}(t))^2 + (T_{22}(t))^2=1
\end{equation}
Iz $4^\circ$ sledi
$$T'_{21}(t)\cdot T''_{21}(t) + T'_{22}(t)\cdot T''_{22}(t)=0 / \int$$
$$\frac{1}{2}(T'_{21}(t))^2 + \frac{1}{2}(T'_{22}(t))^2= C$$
kako to važi za svako $t$, neka je onda $t=0$. Dobijamo
$$\frac{1}{2}1^2 + \frac{1}{2} 0^2=C$$
$$C=\frac{1}{2}.$$
pa važi
\begin{equation}
(T'_{21}(t))^2 + (T'_{22}(t))^2=1
\end{equation}
Iz $(T_{21}(t))^2 + (T_{22}(t))^2=1$ i $(T'_{21}(t))^2 + (T'_{22}(t))^2=1 $sledi
$$T_{21}(t)=\cos \phi (t) $$
$$T_{22}(t)=\sin \phi (t)$$
$$T'_{21}(t)=-\phi'(t) \sin \phi (t) $$
$$T'_{22}(t)=\phi'(t)\cos \phi (t) $$
$$(\phi'(t))^2\sin^2\phi(t)+ (\phi'(t))^2\cos^2\phi(t)=1$$
odnosno
\begin{equation}
(\phi'(t))^2=1
\end{equation}
$$\cos \phi (0) =1 $$
$$\sin \phi (0) =0 $$
$$-\phi(0) \sin \phi (0) =1 $$
$$\phi(0) \cos \phi (0) =1 .$$
Odnosno $\phi(0)=2k\pi$ za neko $k \in Z$ i $\phi'(0)=1$. Otuda, koristeći neprekidnost funkcije $\phi'$, sledi
$$\phi'(t)=1.$$
Dalje,
$$\phi(t)=t+C$$
$$\phi(0)=2k\pi, k\in \mathbb{Z}$$
$$\phi(0)= 0 + C$$
Sledi da je $C=2k\pi, k\in \mathbb{Z}$.
Konačno
$$\phi(t)=t+2k\pi ,$$
pa je
$$T_{21}(t)=\cos (t+2k\pi)=\cos t$$
$$T_{22}(t)=\sin(t+2k\pi)=\sin t.$$
Odnosno
$$F(x,t)=e^x(1\cdot \cos t, \sin t)=(e^x \cos t, e^x \sin t).$$