Диференцијални рачун
Почетна страна »
Функције »
Низови »
Гранична вредност »
Непрекидност функције »
Изводи »
Примена извода »
• Теореме »
• Тејлоров полином »
• Лопиталово правило »
• Монотоност »
• Конвексност »
• Графици функција »
Јована Јездимировић,
Универзитет у Београду, Математички факултет
Примена математичког модела у земљотресном инжењерству
Земљотрес је природна појава настала услед изненадног ослобађања енергије у земљиној кори, која се манифестује као подрхтавање тла. Непосредни узроци настанка земљотреса су: тектонски покрети земљине коре, вулканска активност, рушење карсних стена и слично.
Место у унутрашњости земље, где је дошло до кидања веза између блокова уз претварање потенцијалне енергије у кинетичку (сеизмичку) и одакле полазе сеизмички таласи, назива се хипоцентар земљотреса. Пројекција хипоцентра на земљину површину назива се епицентар. Хоризонтално одстојање било које тачке на Земљиној површини од од епицентра назива се епицентрално растојање, а од хипоцентра хипоцентрално растојање.
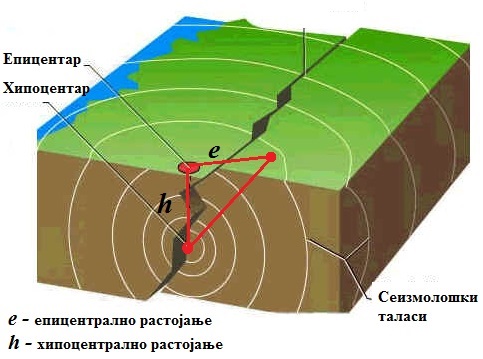
Сеизмички таласи који настају при земљотресу се могу деле на: лонгитудиналне, трансферзалне и површинске (Лaвовe и Рејлијевe) таласе.
Математички модел (примене извода у земљотресном инжењерству) присутан је у одређивању понашања грађевинских конструкција при дејству земљотреса помоћу диференцијалних једначина кретања. Услед дејства земљотреса долази до померања тла и конструкције која се посматра. Јављају се инерцијалне силе индуковане масом и убрзањем померања тла. Конструкција прихвата померање тла и услед инерцијалних сила се креће.
Разматра се дејство спољашње поремећајне силе F(t) на пригушене осцилације система са једним степеном слободе померања. Претпоставља се да је дејство дате поремећајне силе независно од кретања разматраног механичког система и да јој се интензитет мења према хармонијском закону облика:
F(t) = F_0 \sin {pt}.
На основу Далемберовог приниципа (да се динамичка равнотежа сила може посматрати као статичка, ако се додају одговарајуће инерцијалне силе) једначина динамичке равнотеже система је:
my'' + cy' + ky = F _ 0 \sin {pt}
односно:
y'' + 2 \epsilon y' + {\omega }^ 2 y = \frac { F_0 }{ m } \sin {pt}.
Опште рeшење претходне нехомогене диференцијалне једначине је у облику збира општег решења хомогене једначине и партикуларног решења нехомогене једначине:
\newline y = y_h + y_p
\newline
\newline
y = Ce^{- \epsilon t } \sin {( {\omega}_d t + \alpha )} + N_p \sin{ ( pt - \omega ) }.
Део кретања описан датим решењем се брзо амортизује после неколико циклуса осцилација, тако да преостаје само устаљено хармонијско кретање одређено једначином:
y = N_p \sin{ ( pt - \omega ) }.
При чему су амплитуда кретања и фазни угао, респективно, једнаки:
N_p = \frac { F _ 0 }{ m \sqrt{( { \omega } ^2 - p ^ 2 ) ^ 2 + 4 { \epsilon } ^ 2 p ^ 2} }
\qquad tg { \phi } = \frac { 2 \epsilon p }{ { \omega } ^2 - p ^ 2 }.
