Tabla de contenidos
• Inicio »
• Historia »
• Integrales »
• Aplicaciones »
• Superficies »
• Ejemplos »
Temas avanzados:
• Longitud de un arco »
• Volumen de un cuerpo »
• Superficie de un cuerpo »
• Ejercicios »
Las integrales
Definición. Sea una función f(x) definida y continua en el intervalo [a, b], con f (x) ≥0, x ∈ [a, b]. Entonces, la superficie de la figura P bajo la curva y = f (x) en el intervalo [a, b] es igual a la integral definida entre [a, b], es decir:
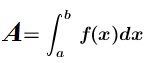
Otro ejemplo:

| 1. Calcular $\int_{0}^{10}{3dx}$. | 2. Calcular $\int_{0}^{4}{xdx}$. | 3. Calcular $\int_{-1}^{1}{dx}$. | 4. ¿Cuál es la correcta? |
