Površina lopte
Lopta je telo ograničeno sferom. Dakle, lopta je skup tačaka u prostoru čije je rastojanje od date tačke manje ili jednako datom broju. Loptu možemo dobiti i obrtanjem polukruga oko njegovog prečnika.
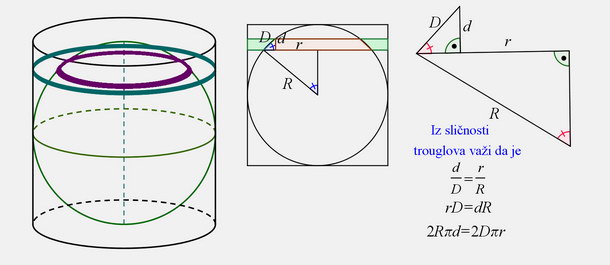
Primetimo da je površina omotača valjka čiji je poluprečnik osnove $r$ i visina $2r,$ $P=4r^2 \pi$. Zamislimo sada da je lopta smeštena u takav valjak i da i loptu i valjak presečemo dvema paralelnim ravnima (koje su paralelne osnovi valjka) čija je udaljenost veoma mala. Između te dve ravni dobijamo prsten na valjku i prsten na sferi. Oba prstena imaju istu površinu! Zašto? Prsten na sferi ima poluprečnik ali je zato širi od prstena na omotaču valjka. Ako je udaljenost između dve ravni jako mala povrčine ta dva prstena bić jednake. Posmatrajmo dva pravougla trougla. Hipotenuza većeg je poluprečnik sfere, a hipotenuza manjeg trougla smanjenjem udaljenosti ravni postaje tangenta pa je normalna na poluprečnik $R$, $D$ je normalna na $R.$ Trouglovi su slični pa su stranice podudarne i sledi $\frac{r}{R}=\frac{d}{D},$ odnosno $rD=Rd.$ Odatle važi $2R\pi d=2r \pi D$, to jest površina prstena na omotaču valjka jednaka je površini odgovarajućeg prstena na sferi. Kako to važi za prstene određene bilo kojim bliskim paralelnim ravnima, sledi da je površina cele lopte jednaka površini celog omotača valjka .
Dakle, površina lopte poluprečnika $R$ jednaka je $P=4 \pi R^2.$ .
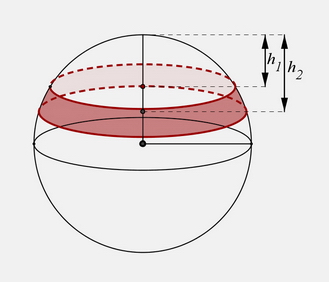
Kada loptu presečemo nekom ravni deo sfere koju tom prilikom dobijemo zovemo kalotom. Površina kalote visine $h$ i prečnika sfere $R$ je $P=2\pi R h.$
Ako neku sferu presečemo dvema paralelnim ravnima, tada se deo sfere izmežu tih dveju ravni naziva sfernim pijasom. Da bismo izračunali površinu sfernog pojasa, možemo koristiti prethodno odbijenu formulu za izračunavanje površine kalote. Pa površinu sfernog pojasa računamo kao razliku površina dveju kalota sfere. Ako visina veće kalote $h_2$ a visina manje $h_1$, tada je površina sfernog pojasa $$P=2\pi R h_2 - 2\pi R h_1=2\pi R(h_2-h_1).$$ Ako sa $h$ označimo rastojanje paralelnih ravni, tada možemo reći da je površina sfernog pojasa visine $h$jednaka $$P=2\pi R h.$$