1. Koliko je $dm^2$lima potrebno za izradu $1000$ zatvarača za flaše, ako je za izradu jednog zatvarača potreban komadić lima kružnog oblika prečnika $3\; cm?$
Izračunajmo površinu jednog zatvarača
$P=\pi \cdot r^2 = 3.14 \cdot 9cm^2= 28,26cm^2 .$
Za hiljadu zatvarača potrebno je $28260 cm^2 ,$ odnosno $282,6 dm^2 .$
Zatvori rešenje.
2. Koliko će se smanjiti površina kruga ako se poluprečnik smanji 3 puta?
Površina kruga pre smanjenja poluprečnika je $P=r^2 \cdot \pi . $
Ako poluprečnik smanjimo $3$puta iznosiće $r_1=\frac{r}{3}$ a površina $P_1 =\frac{r^2}{9} \cdot \pi .$
Dakle, površina će se smanjiti devet puta.
Zatvori rešenje.
3. Odredi površinu kružnog isečka ako je:
1) $r=12\; cm, \quad \alpha=35^{\circ};$
2) $R=2\; cm, \quad \alpha=45^{\circ}.$
$1)$ Površinu kružnog isečka računamo kao
$P= \frac{r^2 \cdot \pi}{360^{\circ}} \alpha = \frac{(12cm)^2 \pi}{360^{\circ}} \cdot 35^{\circ}=14 \pi cm.$
Zatvori rešenje.
 4. Kvadratu čija je površina $256 \; cm^2 ,$ upisan je i opisan krug. Odraditi površinu tako dobijenog kružnog prstena.
4. Kvadratu čija je površina $256 \; cm^2 ,$ upisan je i opisan krug. Odraditi površinu tako dobijenog kružnog prstena.
Odredimo prvo dužinu ivice kvadrata, $a^2 = 256cm^2,$
pa je $a=16cm$ odnosno $r_u=8cm.$
a popuprečnik opisanog kruga je $r_o=\frac{d}{2}=8\sqrt{2}cm .$
Pa računamo površinu prstena:
$P=(r^2_o -r^2_u)\pi =(128cm^2 -64cm^2 )\pi =64 \pi cm^2$
Zatvori rešenje.
5. Prečnik saobraćajnog znaka kružnog oblika je $5,6 \; dm.$ Saobraćajni znak je obojen po obodu, širine $8 \; cm$ crvenom bojom, a ostalo žutom. Koliko $kg$ koje boje treba za izradu 1000 takvih znakova, ako je $1\; l$ boje dovoljan za $4 \; m^2 ?$
Poluprečnik znaka iznosi $28cm.$
Površina dela kruga koji je obojen u crveno (kružni prsten)je
$P=(r^{2}_{znak} - r^{2}_{znak-obod}) \pi = (28^2 cm^2 - 20^2 cm^2) \cdot 3,14= 1205,76cm^2 ,$
Ako imamo takvih 1000 znakova ukupna površina je $1205760 cm^2 = 120,5 m^2 .$
Ako za $4m^2$ utrošimo $1l$ boje, za $120m^2$ utrošićemo $\frac{120 l}{4}=30 l$ boje.
Površina dela kruga obojen u žuto (manji krug )je
$P=r^2_{znak-obod} \pi= 20^2 cm^2 \cdot 3,14=1256cm^2 .$
Ako imamo takvih 1000 znakova ukupna površina je $1256000 cm^2 = 125,6 m^2 .$
Ako za $4m^2$ utrošimo $1l$ boje, za $125,6m^2$ utrošićemo $\frac{125,6 l}{4}=31,4 l$ boje.
Zatvori rešenje.
6. Površina kružnog isečka iznosi $36 \pi \; cm^2 ,$ a poluprečnik $24 \; cm.$ Koliki je njegov centralni ugao?
$ P_i =36 \pi cm^2$
$36 \pi cm^2 = \frac{24^2 cm^2 \pi}{360^{\circ}} \alpha $
$36=\frac{576}{360^{\circ}}\alpha$
$\alpha = \frac{360^{\circ} \cdot 36}{576}=22,5^{\circ} .$
Zatvori rešenje.
 7. Krug prečnika $10 \; cm,$ podeljen je na $8$ jednakih isečaka , a drugi krug, prečnika $6\; cm,$ podeljen je na $6$ jednakih isečaka. Koji isečak ima veću površinu i za koliko?
7. Krug prečnika $10 \; cm,$ podeljen je na $8$ jednakih isečaka , a drugi krug, prečnika $6\; cm,$ podeljen je na $6$ jednakih isečaka. Koji isečak ima veću površinu i za koliko?
Površinu isečka većeg kruga računamo kao osminu površine većeg kruga
$P_{i.vk}=\frac{10^2 cm^2 \pi}{8}=12,5 \pi cm^2 .$
Površinu isečka manjeg kruga računamo kao šestinu površine manjeg kruga
$P_{i.mk}=\frac{6^2 cm^2 \pi}{6}=6 \pi cm^2 .$
Veću površinu ima isečak većeg kruga.
Zatvori rešenje.
8. Pekar Vasa peče kolače u obliku kruga i odozgo ih preliva čokoladom. Za površinu od $1\; cm^2$ potrebo je $2 \; g$ čokolade. Koliko će komada keksa Vasa preliti sa $200 \; g$ čokolade ako je prečnik jednog keksa $4 \; cm ?$
Pošto Vasa ima samo 200 grama čokolade , to mu je dovoljno za $100cm^2$kola&3269;a .
Izračunajmo površinu jednog kolača $P=4^2 \pi cm^2=50,24cm^2 .$ Dakle biće dovoljno za skoro 2 klačića .
Zatvori rešenje.
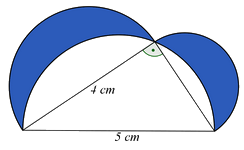 9. Izračunaj površinu osenčene figure.
9. Izračunaj površinu osenčene figure.
Potrebno je da pre svega odredimo nepoznatu katetu pravouglog trougla, primenom pitagorine teoreme dobijamo $x^2=5^2 -4^2 =9 ,$ $x=3.$
Površinu osenčenog dela dobijamo tako što od zbira površina trougla, polovine površine kruga čiji je $r=4$ i kruga čiji je $r=3$ oduzmemo polovinu površine kruga čiji je $r=5$.
$P=P_{\triangle}+\frac{P_{r=4}}{2} +\frac{P_{r=3}}{2} - \frac{P_{r=5}}{2} =$
$ 6cm^2 + 25,12cm^2 + 14,13cm^2 - 39,25cm^2=6cm^2$
Zatvori rešenje.