Površina geometrijskih figura

a) Pošinu kocke računamo kao
$P=6 \cdot a^2=6\cdot 121dm^2= 726dm^2 .$
b) $P=2 \dot (ab + bc + ca)=$ $ 2 \cdot (33cm^2 + 60cm^2 +220cm^2)=$
$2 \cdot 313cm^2= 626cm^2$ Zatvori rešenje.

Pre nego što odredimo površinu kvadra, prvo moramo da sve dužine izrazimo u $cm$.
$a=30cm, b=20cm, c=25cm.$
$P=2\cdot (ab+bc+ca)=2\cdot (600cm^2 +500cm^2 +750cm^2)=$ $=2\cdot 1850cm^2 =3700cm^2 .$ Pošto se u zadatku traži broj kvadratnih decimetara, pretvorimo $cm^2$ u $dm^2 .$
$3700cm^2 = 37dm^2$ kartona. Zatvori rešenje.

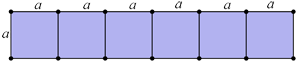Kocka ima 6 strana, ako ih položimo jednu do druge, dobićemo pravougaonik kao na slici. Dužina pravougaonika je $60cm=6a$ odatle zaključujemo da je ivica kocke $a=10cm,$ a površina je $P=6a^2 = 600cm^2 .$ Zatvori rešenje.

Razmislimo prvo da li sve strane treba da popločimo? Dakle ako bazen posmatramo kao kvadar, popločavamo sve strane sem gornje. Pa površina koju treba da popločamo iznosi $P_B =2\cdot 40m \cdot 3m + 2\cdot 30m \cdot 3m + 30m\cdot 40m=$
$=240m^2 + 180m^2 +1200m^2=1620m^2 .$
Izračunajmo površinu pločice $P_P = 10cm \cdot 20cm=200cm^2$
Sada moramo da pretvodimo površinu bazena u $cm^2$ i da je podelimo sa površinom pločice. $1620m^2=16200000cm^2 , $ $\frac{16200000}{200} = 81000$pločica . Zatvori rešenje.