1. Izračunaj površinu prvougaonika ako su njegove strane:
a) $a=11dm, \qquad b=8dm,$
b) $a=11cm, \qquad b=3dm,$
c) $a=2cm \; 8mm , \qquad b=1cm \; 4mm.$
a) Kako se računa površina pravougaonika? $P=a\cdot b$ $P=11dm \cdot 8dm=88dm^2 .$ (Ne zaboravi da pored brojeva pišeš i merne jedinice.) Površina pravougaonika je $88dm^2 .$
b) Pre nego što pomnožiš brojeve proveri da li su dužine stranica izmerene istim merama.
c) Pretvori sve jedinice u milimetre, pa onda računaj.
Zatvori rešenje.
2. Na zemljištu kvadratnog oblika, čija je strana $40m,$ sazidana je kuća oblika pravougaonika dužine $9m$ i širine $6m.$ Kolika je površina zemljišta preostala za dvorište?
Da bi izračunali kolika je površina preostala za dvorište, moramo izračunati kolika je površina zemljišta i površina kuče, a zatim te dve površine oduzeti.
$P_{zemljista}=40m \cdot 40m=1600m^2 ,$ $P_{kuce}=9m \cdot 6m=54m^2 .$ Sada ih oduzmemo:
$P_{dvorista}=P_{zemljista}-P_{kuce}=1600m^2 - 54m^2 = 1546m^2 .$ Površina dvorišta je $1546m^2 .$
Zatvori rešenje.
3. Koliko se cvetova može ubrati sa leje pravougaonog oblika, dimenzija $8m$ i $2m,$ ako se sa svakog kvadratnog metra uberu po $24$ cveta?
Prvo moramo da izračunamo kolika je površina leje. Pošto je leja pravougaoniog oblika, površinu znamo da izračunamo : $P=8m \cdot 2m=16m^2 .$
Ako se sa jednog metra kvadratnog ubere $24$ cveta, onda će sa $16$ metara kvadratna da se ubere $16 \cdot 24=384$ cvetova.
Zatvori rešenje.
4. Kolike mogu biti stranice pravougaonika čija je površina $1a$?
Da bi nam bilo lakše pretvorićemo površinu u metre kvadratne $1a=100m2$. Sada je potrebno da odredimo brojeve $a$ i $b$, takve da je $a\cdot b=100$. To naprimer može biti $a=2, b=50$ ili $a=4, b=25$ ili $a=5, b=20$.. Da li postoji jos neki primer?
Zatvori rešenje.
5. Pod kvadratnog oblika stranice $4m$ treba popločati keramičkim pločicama čije su dimenzije $20 cm$ i $25 cm.$ Koliko pločica treba nabaviti?
Odredimo prvo površinu poda, pošto je kvadratnog oblika, tada je $P_{poda}=4m \cdot 4m=16m^2 .$ Izračunajmo sada površinu jedne pločice $P_{plocice}=20cm \cdot 25cm=500cm ^2 .$ Da bi mogli da odredimo koliko nam je pločica potrebno, moramo podeliti površinu poda sa površinom pločice, a pre toga da izrazimo površinu poda u centimetrima kvadratnim $P_{poda}=16m^2 = 160000 cm^2 .$ Sada ih podelimo $Broj_{plocica}=\frac{P_{poda}}{P_{plocice}}=\frac{160000cm^2}{500cm^2} =800$ plocica.
Zatvori rešenje.
6. Sa jednog ara zemljišta dobije se $100 kg$ krompira. Koliko se krompira dobije sa jedne kvadratne parcele oblika kvadrata stranice $30m?$ Koliko se kilograma dobije sa jednog hektara?
Izračunajmo površinu parcele u arima. $P=30m \cdot 30m=900 m^2 = 9a$
Ako se sa jednog ara dobije $100 kg$, tada se sa devet ari dobije $9 \cdot 100kg= 900kg$ krompira.
$1ha=100a$, sa jednog hektara se dobije $100 \cdot 100kg=10000kg$ krompira.
Zatvori rešenje.
7. Koliko boje treba da se oboje dva zida dimenzija $8m$ i $2m;$ $6m$ i $2m$, ako se za $4m^2 $ utroši $1l$ farbe ?
Izračunajmo površinu oba zida $P_{1}=8m \cdot 2m=16m^2 ,$ $P_{2} = 6m \cdot 2m=12m^2 ,$ $P=P_1 +P_2 =16m^2 + 12m^2=28m^2 .$ Ako nam je za $4m^2$ potreban $1l$, onda nam je za $28m^2$ potrebno $\frac{28m^2}{4m^2}\cdot 1l=7l$ farbe.
Zatvori rešenje.
8. U pravougaonik dužine $8cm$ i širine $6cm$ ucrtan je drugi pravougaonik čije su stranice na rastojanju $1cm$ od stranica prvog pravougaonika. Za koliko je površina prvog pravougaonika veći od površine drugog?
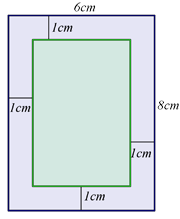Izračunajmo površinu većeg pravougaonika $P_v=8cm \cdot 6cm=48cm^2 .$ A sad prvo odredimo stranice drugog-manjeg pravougaonika, posmatrajmo sliku. Ako su stranice manjeg pravougaonika na rastojanju od $1cm$, tada je svaka stranica manjeg pravougaonika manja za $2cm$ od stranice većeg, pa je površina $P_m=6cm\cdot 4cm=24cm^2 .$ Razlika površina je $P_v -P_m =48cm^2 - 24cm^2 = 24cm^2 .$
2. Na zemljištu kvadratnog oblika, čija je strana $40m,$ sazidana je kuća oblika pravougaonika dužine $9m$ i širine $6m.$ Kolika je površina zemljišta preostala za dvorište?
7. Koliko boje treba da se oboje dva zida dimenzija $8m$ i $2m;$ $6m$ i $2m$, ako se za $4m^2 $ utroši $1l$ farbe ?
Izračunajmo površinu većeg pravougaonika $P_v=8cm \cdot 6cm=48cm^2 .$